ကၽြန္ေတာ္ႏွင္႔ ကဲကုလပ္စ္သခၤ်ာ
ကၽြန္ေတာ္တို႔ေက်ာင္းသူေက်ာင္းသားေတြ ဟာ ငယ္ငယ္ေလးတည္းက ပညာရပ္ေတြ သင္ၾကားခဲ႔ၾကရတယ္ ။ တခ်ိဳ႔ပညာရပ္ေတြ ၊ သီအိုရီေတြက လက္ေတြ႔ မွာအသံုးခ်နိုင္တယ္ ။ တခ်ိဳ႕ ပညာရပ္ေတြ သီအိုရီေတြ ကေတာ႔ ေတြ႔ျမင္ေနရတဲ႔ ပတ္ဝန္းက်င္နဲ႔ဆက္စပ္ၾကည့္လို႔မရဘူး ။ အဲဒီခ်ိန္ဆိုရင္ ကၽြန္ေတာ္တို႔ အမ်ားဆံုး သိခ်င္တဲ႔ေမးခြန္းက ကၽြန္ေတာ္တို႔ဘာေၾကာင္႔ ဒီပညာရပ္ကိုေလ႔လာရတာပါလဲ ဆိုတဲ႔ေမးခြန္းပါပဲ ။ ဆရာသမားေတြကိုေမးၾကတယ္ ။ ကၽြန္ေတာ္တို႔လိုခ်င္တဲ႔အေျဖရသည္လည္းရွိတယ္ မရသည္လည္းရွိတယ္ ။ အဲဒီေတာ႔ကၽြန္ေတာ္တို႔စိတ္ထဲမွာထင္လာတယ္ ။ အဲဒီပညာရပ္ေတြကို စာေမးပြဲအတြက္တင္ပဲ ကၽြန္ေတာ္တို႔ေလ႔လာၾကတာလား။ ဒါမွမဟုတ္ သင္ရိုးညႊန္းတမ္း ကျပဌာန္း ေပးလိုက္လို႔ မ်ား ကၽြန္ေတာ္တို႔ မျဖစ္မေနသင္ေနၾကရတာလား ။ နက္နက္ရွိဳင္းရွိဳင္းစဥ္းစားၾကည့္မယ္ဆိုရင္ ကၽြန္ေတာ္တို႔ ထပ္ကာထပ္ကာ ေလ႔လာသင္ယူေနခဲ႔ရတဲ႔ အေၾကာင္းရာေတြကတကယ္တမ္း လက္ေတြ႔ မွာေရာ အသံုးခ်နိုင္ရဲ့လား။ တခ်ဳိ႔ တခ်ိဳ႕ ေသာ ေက်ာင္းသားေတြကေတာ႔ သူတို႔ရဲ့ အလုပ္ခြင္ျဖစ္တဲ႔ ရူပေဗဒဆုိင္ရာေတြ ၊ ဓာတုေဗဒ ဆုိင္ရာေတြ ၊ စတဲ႔သက္ဆိုင္ရာနယ္ပယ္ေတြမွာ calculus သင္ခန္းစာေတြကို ကို အသံုးခ်ေနၾကပါတယ္ ။ ဒါေပမဲ႔ အားလံုး နီးပါးဟာ ဘာေၾကာင္႔ ဒီပညာရပ္ကို ေလ႔လာတာလဲဆိုတာ ကို သိရွိၿပီးမွ အသံုးခ်ေနၾကတာမဟုတ္ပါဘူး ။ အားလံုးအတြက္လည္း ကကုလပ္စ္ အေၾကာင္းသက္ေသျပဖို႔ မလိုအပ္ပါဘူး ။ ဘာေၾကာင္႔ လဲဆိုေတာ႔ ဒီအလုပ္ဟာ သခ်ာၤပညာရွင္ ေတြသာလွ်င္ လုပ္ရမဲ႔အလုပ္လို႔ ယံုၾကည္ေနၾကလို႔ပါပဲ ။ ဒါဆိုရင္ကၽြန္ေတာ္တို႔က ဘာလို႔မ်ား ကဲကုလပ္စ္ အေၾကာင္းေတြကို ေလ႔လာေနၾကတာလဲ ။
တကယ္ေတာ႔ ကဲကုလပ္စ္ ဟာ အလုပ္တစ္ခုကိုမဝင္ခင္မွာ အလုပ္ရဖို႔အတြက္ ႀကိဳတင္ျပင္ဆင္ တဲ႔ training course တစ္ခုမဟုတ္ပါဘူး ။ ကြန္ပ်ဴတာဘာသာရပ္ေတြလို ဒီဟာကို ဒီလိုေလးလုပ္ ဆိုၿပီးလိုက္လုပ္ၿပီးတက္ေျမာက္သြားတဲ႔ အရာမဟုတ္ဘူး ။ ဒါဝင္ ၊ မာ႔ခ္ ၊ ေဗာ္လ္တိုင္းရား ၊ ေဒါ႔စေတာ႔ရဗ္စကီး တို႔ လို အေတြးအေခၚပိုင္းနဲ႔ဆက္စပ္ၿပီး ေလ႔လာျခင္းတစ္မ်ိဳးပါပဲ ။ ဒီ အေတြးအေခၚ ေတြဟာကၽြန္ေတာ္တို႔ လူေနမွုဘဝေတြရဲ့ အျခခံအစိတ္အပိုင္းေတြ ၊ ကၽြန္ေတာ္တို႔ ကမၻာႀကီးကို ဘယ္လိုယူဆပံုေဖာ္သလဲ ၊ ကမၻာ ေပၚ က ကၽြန္ေတာ္တို႔ရဲ့ ေနရာေတြကိုဘယ္လို သိရွိနိုင္မလဲဆိုတဲ႔ ေမးခြန္းေတြနဲ႔ဆက္စပ္ေနပါတယ္ ။ ကၽြန္ေတာ္တို႔ဟာ ကာ႔ကုလပ္စ္ရဲ့ သေဘာအမွန္ကိုသိနိုင္ဖို႔ဆိုရင္ ကဲ႔ကုလပ္စ္ရဲ့ သမိုင္းေၾကာင္းကိုလည္းထည့္သြင္းေလ႔လာဖို႔လိုပါမယ္ ။ ၿပီးတဲ႔အခါမွာ ကာ႔ကုလပ္စ္မေပၚခင္ကကမၻာႀကီးရဲ့အေျခအေနနဲ႔ကာ႔ကုလပ္စ္ေပၚၿပိးေနာက္ကမၻာႀကီးရဲ့အေျခေနေတြကိုႏွိုင္းယွဥ္သံုးသပ္ရပါမယ္ ။ အဲဒီအခါ မွသာ ကၽြန္ေတာ္တို႔ ကဲကုလပ္စ္ ဘယ္ကျဖစ္လာသလဲ ။ ကၽြန္ေတာ္တို႔ ေက်ာင္းသူေက်ာင္းသားေတြ ကဲကုလပ္စ္ကို ဘာေၾကာင္႔ေလ႔လာဖို႔လိုသလဲဆိုတာ သေဘာေပါက္လာမွာျဖစ္ပါတယ္ ။
ကဲကုလပ္စ္ ဟာ သခ်ာၤရဲ့ အစိတ္အပိုင္းဆိုေတာ႔ သခ်ာၤအေၾကာင္းစ ေျပာၾကည့္ရေအာင္ ။ သခ်ာၤရဲ့ အစက ကုန္သြယ္မွဳကလိုဆိုရလိမ္႔မယ္ ။ ဥပမာ ႏြားတစ္ေကာင္ဟာ ဆိတ္ သံုးေကာင္တန္ဖိုးရွိတယ္ဆိုပါေတာ႔ ။ ႏြားေလး ေကာင္ဆိုရင္ ဆိတ္ ဘယ္ႏွေကာင္စာ နဲ႔ ညီမွ် မလဲ ။ ဒီသေဘာတရားဟာ သခ်ာၤရဲ့ အေျခခံ ေပါင္းႏွဳတ္ေျမွာက္စား နဲ႔ လက္ေတြ႔ နယ္ပယ္နဲ႔ ဆက္စပ္မွဳပါ ။ ဂ်ီၾသေမႀတီ ဆိုရင္လည္း အမွတ္ေတြ ၊ မ်ဥ္းေတြ ၊ ေထာင္႔ ေတြ စတဲ႔ အေၾကာင္းရာေတြနဲ႔ တကယ္႔လက္ေတြ႔ဘဝက အေဆာက္ဦးေတြေဆာက္ရာ မွာ မ်ားစြာအသံုး ဝင္ခဲ႔ၾကပါတယ္ ။ ဒါဟာဘာကိုျပသလဲဆိုေတာ႔ လူေတြ ရဲ့ ပတ္ဝန္းက်င္သဘာဝ မွာျဖစ္ပ်က္ ျမင္ေတြ႔ ေနရတဲ႔ အရာေတြကေနၿပီးသခ်ာၤ နည္းစနစ္ေတြဟာ ျဖစ္ေပၚလာခဲ႔ၾကတယ္ ၊ အသံုးဝင္ ခဲ႔ၾကတယ္ ၊ ဆက္လက္ က်ယ္ျပန္႔လာခဲ႔ၾကတယ္ ဆိုတာကိုေျပာျပေနတာျဖစ္ပါတယ္ ။
ေရွးေဟာင္း ဂရိပညာရွင္ေတြဟာ အေတြးေခၚမွာ အရမ္းကိုထက္ျမက္ခဲ႔ၾကပါတယ္ ၊ ဒါေပမဲ႔ စမ္းသပ္အသံုးခ်မွုမွာေတာ႔အားနည္းခဲ႔ၾကတယ္ ။ ဥပမာ အေနနဲ႔ ျပရမယ္ဆိုရင္ အရစၥတိုလ္တယ္ ဟာ ငွက္ေမႊးထက္ေက်ာက္တံုး က ပိုၿပီးျမန္ျမန္က်တယ္ဆုိတာကိုေလ႔လာေတြ႔ရွိခဲ႔တယ္ ။ ၿပီးတဲ႔ ခါမွာ သူ ေကာက္ခ်က္ခ်လိုက္တာက ေလးတဲ႔အရာ ေတြဟာ ေပါ႔ပါးတဲ႔အရာေတြထက္ ေအာက္ကိုျမန္ျမန္က်တယ္ဆိုတာပါပဲ ။ စမ္းသပ္အသံုးခ်မွဳ မရွိပဲ အေတြးေခၚကေနဆင္းသက္လာတဲ႔ အရစၥတိုလ္တယ္ ရဲ့ အဲဒီအျမင္ဟာ Air resistance ကို ရွာေဖြ မေတြ႔ခင္ ခ်ိန္ထိ ရာစုႏွစ္တိုင္ေအာင္တည္တ႔ံေနခဲ႔တယ္ ။ အခ်ိန္အတိုင္းတာတစ္ခုထိ မွန္ကန္ေနတယ္လို႔ ဆိုနိုင္ပါတယ္ ။ ဒါေပမဲ႔ လက္ေတြ႔စမ္းသပ္ အသံုးခ်မွဳရဲ့ေနာက္ကြယ္မွာေတာ႔ သူ႔အယူအဆေမွးမွိန္ခဲ႔ရတယ္ ။
ေနာက္ထပ္ ကဲကုလပ္စ္ ရဲ့ ပံုျပင္ ဆန္ဆန္ အစိတ္ပိုင္းကေတာ႔ ကာ႔ကုလပ္စ္ဟာ နကၡတ္ေဗဒႏွင္႔ အတူျဖစ္ေပၚလာတယ္လို႔ဆိုပါတယ္ ။ လူေတြဟာ လူေတြေရာက္ရွိေနရာ ေနရာ နဲ႔ လူေတြထိန္းခ်ဳပ္မွဳက လြတ္ကင္းေနတဲ႔ အေျခေနေတြမွာ ေရွ့ျဖစ္လာမဲ႔ အရာေတြကို ႀကိဳတင္ေဟာကိန္းထုတ္နိုင္ဖို႔ ႀကိဳးစားခဲ႔ၾကတယ္ ။ အေမွာင္နဲ႔ ေအးစက္မွဳကိုေၾကာက္တဲ႔လူေတြကိုအေမွာင္နဲ႔အေအးကိုမေၾကာက္ပါနဲ႔လို႔ေျပာမဲ႔အစား၊ေႏြးေထြးတဲ႔အခါလည္းတလွည့္ျပန္လာဦးမွာပါ ။ အရာရာဟာစက္ဝိုင္းပမာပါ ။ ျဖစ္ျပန္ပ်က္ျပန္ ေလာကဓံေပါ႔ ၊ အဆိုးေတြလည္းရွိသလို အေကာင္းေတြလည္းရွိနိုင္ပါေသးတယ္ ။ စတဲ႔အားေပးမွုမ်ိဳးကိုေျပာသင္႔တယ္ ၊ အဲလုိ အားေပးမွဳ မ်ိဳးကလည္း အက်ိဳးေက်းဇူးပုိမ်ားေစတယ္လို႔လူေတြကေတြးေခၚခဲ႔ၾကတယ္ ။
ကမၻာႀကီးဟာ စၾကၤာဝဠာရဲ့အလယ္မွာရွိေနတယ္ ။ ေန႔တစ္ေန႔မွာ ဆိုရင္ ေနမင္းႀကီး က အေရွ့ ကေန ထြက္ၿပီးေတာ႔ အေနာက္ဘက္မွာျပန္ဝင္သြားတယ္ ။ ညတစ္ည မွာဆိုရင္ ၾကယ္အစုေဝးေတြက အေရွ့ကထြက္ၿပီး အေနာက္မွာျပန္ဝင္သြားတယ္ ။ ၾကယ္ေတြဟာ တစ္ခုနဲ႔ တစ္ခု ဆက္ႏႊယ္ၿပီးတည္ရွိေနၾကတယ္ ။ ၿပီးေတာ႔ အဲဒီ ၾကယ္ေတြ ၊ ၿဂိဳလ္ေတြရဲ့ ေရြ႔ လ်ားမွုဟာ တစ္သမတ္တည္းရွိေနတာမဟုတ္ပဲ ေရာေထြးေနတယ္ ။ နကၡတ္ေဗဒ ပညာရွင္ေတြဟာ ၿဂိဳလ္ေတြရဲ့ ေရြ႕လ်ားမွု ကိုေသခ်ာမွတ္သားၿပီးေတာ႔ ေနာက္လာမဲ႔ အနာဂါတ္မွာအဲဒီၿဂိဳလ္ဟာဘယ္ပံုစံေရြ႕လ်ားမလဲဆိုတာ ခန႔္မွန္းၾကတယ္ ၊ ေရြ႕လ်ားမွဳေျပာင္းလဲျခင္းနဲ႔ပက္သက္ၿပီး လူေတြ အေပၚမွာဘယ္လိုသက္ေရာက္မွုရွိလဲ ဆိုတာလည္း မွတ္သားၾကတယ္ ။
၁၅၄၃ ခုႏွစ္မွာေတာ႔ ေကာ႔ပါးနီးကပ္စ္ ဟာ ၿဂိဳလ္ေတြက ကမၻာကိုလွည့္တာမဟုတ္ပဲ၊ ေနကိုလွည့္ ေနတာျဖစ္တယ္ ဆိုတဲ႔ သူ႔ရဲ့ ေလ႔လာခ်က္ ကိုအသံုးျပဳၿပီး ၿဂိဳလ္ေတြရဲ့ ေရြးလ်ားမွဳကို ရိုးရွင္းစြာ ရွင္းျပနိုင္ခဲ႔တယ္ ။ ၿပီးေတာ႔ ကမၻာႀကီးကိုယ္တိုင္ကလည္းပဲ ေနကိုလွည့္ေနတာလို႔ေျပာခဲ႔တယ္ ။ သူ ရွင္းျပခဲ႔တဲ႔ ၿဂိဳလ္ေတြရဲ့ ပတ္လမ္းဟာ စက္ဝိုင္းပံု နီးနီး ျဖစ္ပါတယ္ ။ သူ႔အယူအဆကို church ေက်ာင္းက လက္မခံခဲ႔ဘူး ။ ဘာလို႔လဲဆိုေတာ႔ ဘုရားသခင္ဖန္းဆင္းတဲ႔ ကမၻာေျမဟာ တျခားအရာေတြထက္ အေရးပို မပါသလိုျဖစ္ေနလို႔ ပါ ပဲ ။ အဲဒါေၾကာင္႔လဲေကာ႔ပါးနီးကပ္စ္ ကို church ေက်ာင္းကေနျပစ္ဒဏ္ေပးခဲ႔ပါတယ္ ။
၁၅၈၀-၁၅၉၇ ႏွစ္ေတြမွာေတာ႔ ဘရာ႔ဟဲ ႏွင္႔ သူ႔လက္ေထာက္ ကပ္ပလာ တို႔ဟာ ပိုမိုတိက်တဲ႔ ၿဂိဳလ္ေတြေလ႔လာမွဳ အေျမာက္အမ်ားျပဳလုပ္ခဲ႔ၾကတယ္ ။ ကပ္ပလာ ဟာ အဲဒီေလ႔လာခ်က္ေတြကိုအေျခခံၿပီးေတာ႔ ၁၅၉၆ ခုႏွစ္မွာ ေကာ႔ပါးနီးကပ္စ္ ရဲ့ အယူအဆျပင္ဆင္ခ်က္ကို ထုတ္ျပန္ခဲ႔တယ္ ။ ကပ္ပလာ ဟာ ၿဂိဳလ္ေတြရဲ့ ပတ္လမ္းဟာစက္ဝိုင္းပံုမဟုတ္ပဲ ဘဲဥပံုလမ္းေၾကာင္း (ellipses) ျဖစ္တယ္ဆိုတာျပသခဲ႔တယ္ ။ ေျမာက္မ်ားစြာေသာ ၿဂိဳလ္ေတြေရြ႕လ်ားမွဳနဲ႔ပက္သက္ၿပီး ရိုးရွင္းၿပီး တိက် တဲ႔ နိယာမ ၃ ခုကို ကပ္ပလာ က ထုတ္ျပန္ခဲ႔တယ္ ။
(၁) ေနကိုဦးတည္လည္ပတ္မွဳနဲ႔အတူ ၿဂိဳလ္ေတြရဲ့ပတ္လမ္းဟာ ဘဲဥပံုျဖစ္တယ္ ။
(၂) ေနႏွင္႔ ၿဂိဳလ္ ေတြၾကားမွာ ရွိတဲ႔ အကြာေဝးကို ဆန္႔ထုတ္ဖို႔ အတြက္ေျပာင္းလဲတဲ႔ ၿဂိဳလ္ ရဲ့ အလ်င္ ဟာ ပံုမွန္ႏွဳန္း(ကိန္းေသႏွဳန္း) နဲ႔ တိုးတိုးသြားတယ္ ။
(၃) ပတ္လမ္းအတြက္ၾကာခ်ိန္ ႏွစ္ဆ ဟာ ေနနဲ႔ ၿဂိဳလ္ရဲ့ ၾကားက ပ်မ္းမွ်အကြားေဝး ၃ ဆ နဲ႔ အခ်ိဳးညီတယ္။
ဆိုတဲ႔ နိယာမ ၃ ခုျဖစ္ပါတယ္ ။
၁၆၀၉ ခုႏွစ္မွာေတာ႔ ဂယ္လီလီယို ဟာ စပိုင္ဂလက္စ္(spyglass) ကိုတီထြင္ခဲ႔တယ္ ။ အဲဒီအခ်ိန္တုန္းကေတာ႔ လူသိမ်ားတဲ႔ ပစ္စည္းတစ္ခုေပါ႔ ။ စပိုက္ဂလက္စ္ကို တယ္လီစကုတ္ အေနနဲ႔ အသံုးခ်ၿပီး ေကာင္းကင္ဘံုကုိ ေလ႔လာခဲ႔ၾကတယ္ ။ ဂယ္လီလီယို ဟာ သာမန္မ်က္စိေတြ နဲ႔ မျမင္ေတြ႔ နိုင္တဲ႔ ေျမာက္မ်ားစြာေသာ ေန ၊ လ ၊ ၿဂိဳလ္ နဲ႔ နကၡတ္ ေတြကို ေလ႔လာခဲ႔တယ္ ။ အဲလို သူ ေလ႔လာတဲ႔အခါမွာ ဂ်ဴပီတာၿဂိဳလ္ရဲ့ ၿဂိဳလ္ရံလဟာ ဂ်ဴပီတာၿဂိဳလ္ကို လွည့္ပတ္ ေနတာ သူရွင္းရွင္းလင္းလင္းေတြ႔ခဲ႔ရတယ္ ။ ဒီအခ်က္ ဟာ ကိုပါးနီးကပ္စ္ ထုတ္ေဖာ္ခဲ႔တဲ႔ အရာတိုင္းက ကမၻာကို ခ်ည္းပဲ လွည့္ပတ္ေနတာမဟုတ္ဘူးဆိုတဲ႔ အယူအဆရဲ့ ရိုးရွင္းခိုင္မာတဲ႔ အေထာက္ထား ျဖစ္တယ္ ။ ကိုပါးနီးကပ္စ္ တုန္းကလိုပဲ church ေက်ာင္း ကေနၿပီးေတာ႔ ဂယ္လီလီယို ကိုပစ္ဒဏ္ေပးခဲ႔တယ္ ။ ဒါေပမဲ႔ သူ႔ရဲ့အယူအဆကေတာ႔ တစ္ကမၻာ လံုး မွာရပ္တန္႔လို႔ မရေတာ႔ေလာက္ေအာင္ တစ္ႀကိမ္တည္းျပန္႔ႏွံ႔သြားခဲ႔တယ္။
ဂယ္လီလီယို ဟာ ကမၻာဆြဲအားနဲ႔ ပက္သက္ၿပီးေတာ႔လည္း တုိင္းတာနိုင္ဖို႔ စမ္းသပ္ခဲ႔တယ္။ အရစၥတိုတယ္လ္ ရဲ့ ပိုေလးတဲ႔အရာဝထၳဳက ေပါ႔တဲ႔ အရာထက္ ေအာက္ကိုျမန္ျမန္က်တယ္ ဆိုတဲ႔ အယူအဆကိုမွားယြင္းေၾကာင္း လက္ေတြ႔ျပသခဲ႔တယ္။ သူဟာ အရြယ္စားမတူညီတဲ႔ ေဘာလံုးေလးေတြကို ေလွ်ာေဇာက္မွာလိွမ္႔ခ်ၿပီးေတာ႔ ေအာက္ ကိုက်ဖုိ႔ ၾကာတဲ႔ အခ်ိန္ကိုေသခ်ာ မွတ္သားျခင္း ျဖင္႔ စမ္းသပ္ခဲ႔တယ္ ။ ေနာက္ထပ္ ၁၀ ေပါင္ဆီေလးတဲ႔ အရာဝထၳဳ ၃ ခုကို ေမွ်ာ္စင္ေပၚကေန ပစ္ခ်လိုက္တဲ႔အခါမွာ အားလံုးက ေျမႀကီးေပၚကို တခ်ိန္တည္းမွာက်ေရာက္သြားၾကတယ္ ။ ထပ္ၿပီးေတာ႔ အရာဝထၳဳ ၃ ခုတည္းက ၂ ခုကို ႀကိဳး တိုတို တေခ်ာင္းနဲ႔ ဆက္သြယ္ခ်ည္ေႏွာင္ၿပီး ပစ္ခ်လိုက္တဲ႔အခါမွာလည္း အရာဝထၳဳေတြဟာ ေျမႀကီးေပၚကိုအတူတူ က်သြားၾကတယ္ ။ ေနာက္ တတိယအႀကိမ္မွာေတာ႔ ႀကဳိးအစား စူပါဂလူး ကိုသံုးၿပီးေတာ႔ အရာဝထၳဳ ၂ ခုကို ေကာ္နဲ႔ပူးကပ္ၿပီးေတာ႔ ပစ္ခ်လိုက္တဲ႔အခါမွာ နဂို ၁၀ ေပါင္ရွိတဲ႔ အရာဝထၳဳ ၃ ခု ဟာ ေျမႀကီးေပၚကိုအတူတူက်သြားၾကတယ္ ။ ဒါေပမဲ႔ ေကာ္ေတြေျခာက္သြားၿပီျဖစ္လို႔ နဂို ၁၀ ေပါင္ စီရွိေနတဲ႔ အရာဝထၳဳ ၃ ခုကေနၿပီးေတာ႔ ေပါင္၂၀ ေလးတဲ႔အရာဝထၳဳတစ္ခု နဲ႔ ၁၀ ေပါင္ေလးတဲ႔အရာဝထၳဳ တစ္ခုျဖစ္ေနတာကို ေတြ႔ခဲ႔ရတယ္ ။ အဲဒါေၾကာင္႔ပဲ ဂယ္လီလီယို ဟာ အရစၥတိုတယ္လ္ ေျပာခဲ႔တဲ႔ ပုိေလး ေလး ေအာက္ကိုျမန္ျမန္က်ေလဆိုတဲ႔ ယူဆခ်က္ကုိ မွားယြင္းေၾကာင္း ေျပာခဲ႔တာပဲျဖစ္ပါတယ္ ။
အဲလိုနဲ႔ပဲ ကာကုလပ္ရယ္လု႔ိျဖစ္ေပၚလာမဲ႔ အေျခခံအေတြးေခၚေတြဟာရာစုႏွစ္မ်ားစြာ လည္ပတ္ေနခဲ႔တယ္ ။ ဒါေပမဲ႔ အဲဒီ အယူအဆေတြကို ထုတ္ျပ မဲ႔ လူ ၂ ေယာက္ထက္ၿပီးထြက္ေပၚလာခဲ႔တယ္ ။ အဲဒီလူေတြကေတာ႔ နယူတန္ (Newton) နဲ႔ လစ္ဘနစ္စ္ (Leibniz) တို႔ပါပဲ။ သူတို႔ ၂ ေယာက္ဟာ ေခတ္ကာလတစ္ခုတည္းမွာပဲ တစ္ဦးခ်င္းစီ တစ္ေနရာစီမွာ ကာ႔ကုလပ္စ္ရဲ့ အေျခခံ သီအိုရီ ေတြကို ေလ႔လာခဲ႔တယ္ ။ နယူတန္ နဲ႔ လစ္ဘနစ္စ္ တို႔ဟာ ကာကုလပ္စ္ကုိ ၂ ေယာက္စလံုးတီထြင္ခဲ႔ၾကတယ္ဆိုေပမဲ႔ နယူတန္ဟာပိုၿပီးေတာ႔ လုပ္ေဆာင္နိုင္ခဲ႔တယ္ ။ Derivative ဆိုတာ ေျပာင္းလဲတဲ႔ႏွုန္းပါပဲ ။ ကမၻာေပၚမွာျဖစ္ျဖစ္ သမွ် ၊ ရွိရွိသမွ် အရာအားလံုးဟာ အခ်ိန္တိုင္းနဲ႔ အမွ် ေျပာင္းလဲေနပါတယ္ ။ ဒါေၾကာင္႔လဲ derivatives ဟာမ်ားစြာအသံုးဝင္လာပါတယ္ ။ ၁၆၈၇ ခုႏွစ္မွာေတာ႔ နယူတန္ဟာ three law of motion ေရြ႕လ်ားျခင္းနိယာမသံုးမ်ိဳးကို ခ်ျပခဲ႔ပါတယ္ ။အဲဒီနိယာမေတြကို ရူပေဗဒ ရဲ့ အေျခခံ နိယာမေတြအျဖစ္လည္း လူသိမ်ားပါတယ္ ။
နိယာမ (၁)
အရာဝထၳဳေတြေပၚမွာ သက္ေရာက္တဲ႔အား (ေျမဆြဲအားနဲ႔ ပြတ္တိုက္အားမပါဝင္)မရွိဘူးဆိုရင္ အဲဒီအရာဝထၳဳေတြဟာ ပံုမွန္ အလ်င္(velocity) နဲ႔ပဲ ေရြ႕လ်ားေနမယ္ ။ (constant speed နဲ႔ သူ႔ရဲ့ဦးတည္ရာတိုင္းေရြ႕လ်ားေနတာျဖစ္နိုင္သလို ၊ ရပ္ေနတာ ၊ ထိုင္ေနတာမ်ိဳးလည္းျဖစ္နိုင္ပါတယ္)
ပထမ နိယာမရဲ့ ဥပမာေလးၾကည့္ၾကည့္ပါ ။ တကယ္လို႔သာ သက္ေရာက္တဲ႔အား မရွိခဲ႔ဘူးဆုိလွ်င္ ( f=0 ) အခ်ိန္ တိုင္းမွာေျပာင္းလဲမဲ႔ အလ်င္ (dv/dt) ကလည္း သုညပါပဲ တဲ႔ ။
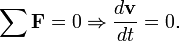
နိယာမ (၂)
အရာဝထၳဳတစ္ခုေပၚမွာသက္ေရာက္တဲ႔အား(f)ဟာ အဲဒီအရာဝထၳဳရဲ့ အေလးခ်ိန္ (m) ႏွင္႔ အရွိန္္(a) တို႔ေျမွာက္ျခင္းနဲ႔ ညီပါတယ္ ။
ဒုတိယနိယာမရဲ့သခ်ာၤဆိုင္ရာဥပမာေလး ၾကည့္ၾကည္ပါ ။
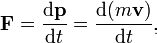
အရာဝထၳဳေပၚမွာသက္ေရာက္တဲ႔အားဟာ အဲဒီအရာဝထၳဳရဲ့ အခ်ိန္တိုင္းမွာေျပာင္းလဲသြားမဲ႔ linear momentum(p) နဲ႔ညီတယ္လို႔ ပထမေျပာပါတယ္ ။ အဲဒီ momentum ဟာ mass times velocity ဆိုတဲ႔ (mv) အခ်ိန္တိုင္းမွာျဖစ္ေပၚေျပာင္းလဲမဲ႔ အေလးခ်ိန္နဲ႔ အလ်င္ တ႔ိုႏွင္႔ ညီပါတယ္ ။
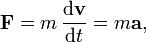
အလ်င္သာ အခ်ိန္တိုင္း အခ်ိန္တိုင္းမွာ ကိန္းရွင္အေနနဲ႔ ေျပာင္းသြားမယ္ အရာဝထၳဳရဲ့ အေလးခ်ိန္ (mass) ကေတာ႔ ဒီတိုင္းပါပဲ ။ ဒါေၾကာင္႔ f=m dv/dt လို႔ ေရးတာပါ ။ အခ်ိန္တိုင္း အခ်ိန္တိုင္း မွာ ေျပာင္းလဲမဲ႔ အလ်င္ဟာ အဲဒီအရာဝထၳဳရဲ့ အရွိန္ ပါပဲ ။ ဒါေၾကာင္႔ dv/dt = a ပါ ။ ေနာက္ဆံုးမွာေတာ႔ ဒုတိယ နိယာမ ေဖာ္ျမဴလာျဖစ္တဲ႔ f=ma ဆိုတာကို ရလာတာျဖစ္ပါတယ္ ။
နိယာမ (၃)
အရာဝထၳဳ ၂ ခုအခ်င္းခ်င္းတစ္ခုေပၚတစ္ခု သက္ေရာက္တဲ႔အားဟာ ပမဏတူညီၿပီးေတာ႔ ဦးတည္ရာ မတူဘူး ။
ၿဂိဳလ္ေတြရဲ့ ေရြလ်ားမွဳကို ရွင္းျပနိုင္ဖို႔အတြက္ေတာ႔ နယူတန္ဟာ သူ႔ရဲ့ အေျခခံ နိယာမ ၃ ခုကႏွင္႔ ေျမဆြဲအားနိယာမ ကို ေပါင္းစပ္အသံုးျပဳခဲ႔ပါတယ္ ။
ေျမဆြဲအားနိယာမ
အရာဝထၳဳ ႏွစ္ခု ၾကားမွာရွိတဲ႔ ေျမဆြဲအားဟာ အဲဒီအရာဝထၳဳ ႏွစ္ခုရဲ့ အေလးခ်ိန္ေတြ ေျမွာက္ျခင္းနဲ႔ တိုက္ရိုက္အခ်ိဳးက်ၿပီးေတာ႔ ၊ အရာဝထၳဳႏွစ္ခုၾကားမွာရွိတဲ႔ အကြာေဝး ၂ ဆ နဲ႔ ေျပာင္းျပန္အခ်ိဳးက်တယ္။
နယူတန္ရဲ့ နိယာမ ေတြဟာ က ကပ္ပလာ နိယာမေတြထက္ ပိုမိုရုိးရွင္းၿပီးနားလည္ရလြယ္ကူေစပါတယ္ ။ ဒါေပမဲ႔လည္း အဲဒီ နိယာမေတြဟာ ကပ္ပလာရဲ့ ေတြးေခၚမွဳ ရလဒ္ ေတြလို႔လည္းဆိုနိုင္ပါတယ္ ။
နယူတန္ရဲ့ စၾကာဝဠာသေဘာဟာ တခါတေလမွာ ခ်ိန္သီးနာရီေတြရဲ့ အလုပ္လုပ္ပံုကဲသုိ႔ေဖာ္ျပၿပီးေတာ႔ ဘာခ်ိန္မွာဘာျဖစ္မယ္ ၊ ဘာေတြျဖစ္လိမ္႔မယ္ဆိုတာ ႀကိဳတင္ေဟာကိန္းထုတ္နိုင္တယ္လို႔ဆိုပါတယ္ ။ ကၽြန္ေတာ္တို႔ ဟာ ဘိလိယက္ေဘာလံုးေလးေတြ အခ်င္းခ်င္းထိတိုက္ၿပီး ဘယ္ေနရာကုိေရြ႕မယ္ဆိုတာ ႀကိဳတင္မွန္းဆနိဳင္သလုိပါပဲ ။ ေယဘုယ်အားျဖင္႔ေတာ႔ ကၽြန္ေတာ္တို႔ဟာ ဟန္ပန္ ၊ သ႑န္ေတြ တူညီမွုကိုၾကည့္ၿပီးခန္႔ မွန္းနုိင္ၾကတာပါ ။ ၿဂိဳလ္ေတြဟာလည္း ဘိလိယက္ေဘာေတြလို ပံု သ႑န္ေတြ ႏွင္႔ ေရြ႕လ်ားမွုေတြ တူညီေနပါတယ္ ။
ရုတ္တရက္ဆိုသလိုပဲ အာကာသ မွာရွိေနတဲ႔ ရွဳပ္ေထြးလွတဲ႔ ေရြ႕လ်ားမွုေတြကေန သခ်ာၤနည္းစနစ္ေတြရဲ့ ရိုးရွင္းတဲ႔ ဆင္႔ကဲေျပာင္းလဲမွဳေတြအျဖစ္ျပသနိုင္ခဲ႔ပါတယ္ ။ ဒါဟာလူသားေတြရဲ့ နားလည္နိုင္မွဳ ကို ပိုမို ယံုၾကည္ေစခဲ႔တာပါပဲ ။ ကမၻာရဲ့ ပတ္ပတ္လည္ကို ထိန္းခ်ဳပ္နိုင္ဖို႔ စြမ္းရည္ေတြလည္းရရွိေစခဲ႔တယ္ ။ ကပ္ပလာနဲ႔ နယူတန္ တို႔ရဲ့ ေတြ႔ ရွိမွုဟာ နကၡတ္ ေဗဒ တစ္ခုတည္းတင္ေျပာင္းလဲေစခဲ႔တာမဟုတ္ပဲ ၊ စၾကၤဝဠာနဲ႔ပက္သက္ၿပီး လူေတြရဲ့ ယူဆခ်က္အျမင္ေတြကိုပါေျပာင္းလဲေစခဲ႔တယ္ ။
နယူတန္ရဲ့ ေလ႔လာေတြ႔ရွိခ်က္ဟာ ႀကီးက်ယ္ခမ္းနားေပမဲ႔လည္း ၿပီးျပည့္စံုသြားတာေတာ႔မဟုတ္ပါဘူး။ နယူတန္ရဲ့ နိယာမ ဟာ ေျမဆြဲအား အေၾကာင္းကို ျပည့္စံုေအာင္ရွင္းမျပနိုင္ခဲ႔ပါဘူး ။ နယူတန္ဟာ ေျမဆြဲအားရဲ့ ပမာဏ ဘယ္ေလာက္ရွိသလဲဆိုတာ သခ်ာၤ နည္းအရာ တိတိ က်က် ျဖစ္ေအာင္ ကိုတြက္ထုတ္ျပခဲ႔ပါတယ္ ။ ဒါေပမဲ႔ ကမၻာေျမဆြဲအားဘာေၾကာင္႔ျဖစ္ေစ သလဲ ဆိုတာကိုေတာ႔ သူရွင္းမျပနိုင္ခဲ႔ပါဘူး ။ ကမၻာေျမရဲ့ဆြဲအားဟာဘယ္လိုမ်ိဳးပါလဲ ၿဂိဳလ္တစ္ခုနဲ႔တစ္ခုၾကားမွာ ႀကိဳလိုမ်ိဳးတြယ္ဆက္ၿပီး တစ္ခုႏွင္႔တစ္ခု ဆြဲေနၾကတာမ်ိဳးလား ။ သံုးသပ္ၾကည့္ရတာကေတာ႔ အဲလိုမျဖစ္နိုင္ပါဘူး ။ ေျမဆြဲအားဘယ္လို အလုပ္လုပ္လဲဆိုတာ ယခုေခတ္အခ်ိန္ခါမွာေတာ႔ ပိုသိလာၾကပါၿပီ ။ ဒါေပမဲ႔ နယူတန္ ေခတ္တုန္းကေတာ႔ ဒါကိုမသိခဲ႔ၾကေသးပါဘူး။ဒါေၾကာင္႔လည္းနယူတန္ ေျမဆြဲအားနိယာမကို ေဖာ္ထုတ္တဲ႔အခါမွာသြယ္ဝိုက္ၿပီးထုတ္ခဲ႔တာပဲျဖစ္ပါတယ္ ။ ကၽြန္ေတာ္တို႔ အသံုးျပဳ နိုင္ဖို႔ အတြက္ဆိုရင္ေတာ႔ အရာရာ တိုင္းကို ၿပီးျပည့္စံုေအာင္ ရွင္းလင္းဖို႔မလိုအပ္လွပါဘူး။ ဒါဟာ နည္းပညာ (technology) ႏွင္႔ သိပၸံပညာ (Science) ေတြအတြက္ ဆင္႔ကဲ ေျပာင္းလဲျခင္းေတြျဖစ္ေပၚေစတဲ႔ အခ်က္ေတြပါပဲ ။
ကဲ႔ကုလပ္စ္ဆိုတာလည္း အဲဒီအတိုင္းပါပဲ ။ နယူတန္နဲ႔ လစ္ဘနစ္စ္ တို႔ဟာ ေယဘုယ်ဖန္ရွင္ေတြကိုဘယ္လို derivates လုပ္ရမယ္ဆိုတာကို ေကာင္းေကာင္းသိခဲ႔ၾကပါတယ္။ ဒါေပမဲ႔ derivative ရဲ အဓိပၸါယ္ဖြင္႔ဆိုခ်က္ကိုေတာ႔ တိတိ က်က် မေျပာျပခဲ႔ၾကဘူး ။ သူတို႔ဟာသူတို႔အသံုးျပဳ ခဲ႔တဲ႔ သီအိုရမ္ေတြကို တကယ္မေျဖရွင္းနိုင္ခဲ႔ၾကဘူး ။ သူတို႔ရဲ့ေဖာ္ျပခ်က္ေတြဟာရွင္းျပခ်က္ေတြမဟုတ္ဘူး ။ သူတို႔ဟာ derivative ကို အလြန္အလြန္ေသးငယ္တဲ႔ ဂဏန္း၂ ခုရဲ့ စားလဒ္ အျဖစ္ပဲ ရွင္းျပခဲ႔ၾကတယ္ ။ (ဥပမာ ..အဲဒီဂဏန္းေတြဟာ အဆံုးဆမရွိ ေသးငယ္တယ္ ၊ ဒါေပမဲ႔ သုညလည္းမဟုတ္ျပန္ဘူး)အဲဒီရွင္းလင္းေဖာ္ျပခ်က္ဟာအဲဒီအခ်ိန္ကသခ်ာၤပညာရွင္ေတြကိုသိပ္ၿပီးသေဘာမေတြ႔ေစခဲ႔ပါဘူး ။ ဒါေပမဲ႔လည္း နယူတန္ နဲ႔ လစ္ဘနစ္စ္ တို႔ရဲ့ တြက္ခ်က္မွဳ နည္းလမ္းဟာ အေျဖ မွန္ ထြက္ဖို႔ အတြက္ေတာ႔ အမွားေထာက္ျပစရာမရွိေလာက္ရွင္းလင္းနိုင္ခဲ႔ပါတယ္ ။
ေနာင္ ႏွစ္ေပါင္း ၂၀၀ ေလာက္ၾကာၿပီးတဲ႔ေနာက္မွာေတာ႔ ဂ်ာမန္ သခ်ာၤပညာရွင္ ဝဲရာစထရက္စ္ (Weierstrass- 1815 –1897) ႏွင္႔ ျပင္သစ္သခ်ာၤပညာရွင္ ေကာ႔ေခ် (Cauchy-၁၇၈၉-၁၈၅၇) တို႔ ကေတာ႔ ကဲကုလပ္စ္ရဲ့ နည္းစနစ္တစ္မ်ိဳးျဖစ္တဲ႔ (epsilons and deltas) ဆိုတဲ႔ ပိုေကာင္းတဲ႔ စနစ္ ကို ထုတ္ေဖာ္နိုင္ခဲ႔ပါတယ္ ။ ဒယ္လ္တာနဲ႔ အပ္စလြန္ နည္းကေတာ႔ ေသးငယ္တဲ႔ ဂဏန္းပမာဏကို လက္ေတြျပသနိုင္ဖို႔ နည္းစနစ္ပါ ။
၁၉၆၀ ခုႏွစ္မွာေတာ႔ ယုတၱိေဗဒ ပညာရွင္ ေအဗရာဟမ္ ရိုဘင္ဆမ္ ဟာ အလြန္တိုေတာင္းတဲ႔အခ်ိန္ပမာဏေလး(infinitesimals)အာရံုခံေဖာ္ျပနိုင္မဲ႔နည္းလမ္းကိုေတြ႔ရွိခဲ႔ပါတယ္ ။ ဒါသာသခ်ာၤဘာသာရပ္ရဲ့ အစိတ္အပိုင္းအသစ္ျဖစ္တဲ႔ nonstandard analysis ပါပဲ ။ nonstandard analysis ဟာ calculus ေတြ ၊ differential equation ေတြ ႏွင္႔ ၄င္းတို႔နဲ႔ဆက္ႏႊယ္ေနတဲ႔ အေၾကာင္းအရာေတြကို နားလည္နိုင္ဖို႔ ပိုေကာင္းတဲ႔နည္းလမ္းတစ္ခုပါပဲ။ ဒီနည္းလမ္းဟာ ဘယ္လိုပံုစံလဲဆိုေတာ႔ အေၾကာင္းရာတစ္ခုကို အေျခေန ၊ ရွင္းျပခ်က္ေတြ နဲ႔ သိတာထက္ မသိစိတ္ကေန အလိုလိုသိတဲ႔ ၊ ဝမ္းတြင္းသိ အေနနဲ႔လက္ခံလိုက္တာမ်ိဳးပါ ။ နယူတန္နဲ႔ လစ္ဘနစ္ဇ္ တို႔ဟာ ကဲကုစ္လဗ္ စ္ ကို စိတ္ထဲကအေနအလိုလိုသိေနၾကတယ္လို႔ယူဆလိုက္တာမိ်ဳးပါ။အေျခခံအားျဖင္႔ ေတာ႔ ဒါဟာ infinitesimal approach ႏွင္႔ epsilon-delta approach တို႔ရဲ့ အႀကီးမားဆံုးကြားျခားခ်က္ပါပဲ ။
Delta-epsilon နည္းလမ္းမွာဆိုရင္ ဂဏန္းေတြဟာ သတ္မွတ္တဲ႔ အရြယ္အစားတစ္ခုရွိၾကတယ္။ ေတြးၾကည့္မယ္ဆိုရင္ပမာဏတစ္ခုရွိတဲ႔ဂဏန္းဟာလံုးဝအေသးငယ္ဆံုးေတာ႔မဟုတ္ေသးဘူး။ထပ္ၿပီးေျပာင္းလဲနိုင္ေသးတဲ႔ေသးငယ္မွဳမ်ိဳးပဲ ။ ဥပမာတစ္ခုေပါ႔ တစ္ရဲ့ တစ္သန္းပံုပံု တစ္ပံု ရွိတဲ႔ ပမာဏေလးဆိုပါေတာ႔ ။ အဲဒီဂဏန္းေလးကို အေသးဆံုး ျဖစ္ေအာင္ဆက္လုပ္မယ္ဆိုရင္ ဘာေတြျဖစ္လာမလဲ ။ ဒီဂဏန္းဟာ ေျပာင္းလဲသြားမယ္ ။ အဲလိုေျပာင္း လဲေနတာဟာ montion တစ္ခု action တစ္ခု လို႔ဆိုနိုင္မလား ။ ကကုလဗ္စ္ရဲ့ သေဘာတရားက အခ်ိန္တိုင္းအခ်ိန္တိုင္း ၊ အေရြးတိုင္းအေရြ ႔တိုင္းမွာ ေျပာင္းလဲ မွဳကိုသိနိုင္ဖို႔အတြက္ အေသးငယ္ဆံုး ခ်ံဳ႕ၿပီး တြက္ခ်က္တာ ပါ ။ အေသးငယ္ဆံုးျဖစ္ေအာင္ခ်ံဳ႕တဲ႔ေနရာမွာလဲ ေျပာင္းလဲသြားနိုင္တယ္ ။
ဒါေၾကာင္႔ နယူတန္ ၊ လစ္ဗနစ္ နဲ႔ ရိုဘင္ဆမ္ တို႔ဟာ လံုးဝ ထပ္ေသးစရာမလိုေတာ႔တဲ႔ အေသးဆံုး ဂဏန္း infinitesimals အျဖစ္ စိတ္ထဲမွာသတ္မွတ္လိုက္တာပါ ။ ဒါဆိုရင္ အဲဒီဂဏန္းဟာ ထပ္ၿပီး ေသးေအာင္ေျပာင္းလဲဖို႔မလိုေတာ႔ပါဘူး ။ ဘယ္လိုလဲဆိုေတာ႔ အေသးငယ္ဆံုးေသာဏဂန္း ဒါေပမဲ႔ ပမာဏေတာ႔ေဖာ္ျပလို႔ မရဘူးဆိုတဲ႔ပံုစံေပါ႔ ။ ဒါဟာ သခ်ာၤရဲ့ ႀကီးမားတဲ႔ အစိတ္ပိုင္းသစ္ပါပဲ ။
၁၉ ရာစုေႏွာင္းပိုင္းမွာေတာ႔ ေဂ်ာ႔ခန္တား(Georg Cantor) ဟာ infinity ဆိုတဲ႔ ေဝါဟာရတစ္ခု ႏွင္႔ သူ႔ရဲ့ အယူအဆေတြ ကို ထုတ္ေဖာ္ခဲ႔ပါတယ္ ။ ခန္းတား ဟာ convergence of Fourier series ကိုေလ႔လာခဲ႔တယ္ ။ အေစာပိုင္းသခ်ာၤပညာရွင္ေတြဟာ တူညီတဲ႔ အစုေတြ ျပဳၿပီးေတာ႔ ပဲ မေရမတြက္နိုင္တဲ႔ ဂဏန္း ေတြကိေဖာ္ျပၾကတယ္ ။ ဒါေပမဲ႔ ခန္းတား ကေတာ႔ အဲေလာက္နဲ႔ရပ္မထားပါဘူး ။ တကယ္လို႔ sets ေတြမွာ ပါဝင္တဲ႔ elements အေရအတြက္ (cardinality) သာတူညီခဲ႔မယ္ဆိုရင္ အဲဒီ set ေတြကို အခ်ိဳးခ်ၿပိးေတာ႔လည္းေရးနိုင္ပါေသးတယ္ ။အဲဒီလိုေဂ်ာ႔ခန္းတား ဟာ infinity set ႏွစ္ခုကို အခ်ိဳးခ်လိုက္တဲ႔ ေနာက္ပိုင္းမွာ ေတာ႔ ကၽြန္ေတာ္တို႔ မ်က္ျမင္ နဲ႔ ေရတြက္နိုင္မဲ႔ countable numbers ႏွင္႔ အတူ မ်က္ျမင္နဲ႔ ေဖာ္ျပလို႔ မရတဲ႔ uncountable numbers ေတြပါရွိေသးတယ္ဆိုတာကိုလူေတြ လက္ခံလာၾကပါတယ္။
သက္ေသျပနိုင္တဲ႔ နည္းစနစ္ေတြ တိုးတက္လာတာနဲ႔ အမွ် သခ်ာၤရဲ့ အခန္းက႑ဟာလည္းပိုၿပီးအေရးပါလာခဲ႔တယ္ ။ ပိုၿပီးေတာ႔ လက္ေတြ႔နယ္ပယ္နဲ႔ ဆက္စပ္လာနိုင္တယ္ ၊ ပိုၿပီးေတာ႔လည္းတိက်လာၾကတယ္ ။ ဒီကေန႔ ကၽြန္ေတာ္တို႔ ရဲ့ သခ်ာၤအဆင္႔အတန္းဟာေတာ႔ အလြန္ကိုျမင္႔မားေနပါၿပီ ။ ဒါဟာ ဘယ္ကေနျဖစ္ေပၚလာရသလဲဆိုရင္ “ အေၾကာင္းျပခ်က္ ရွာေဖြျခင္းအတက္ပညာကေနရရွိလာတာပါ ” ။ ရုပ္ပုိင္းဆိုင္ရာ ေလ႔လာမွဳကေနေတြ႔ရွိခဲ႔တာမဟုတ္ပါဘူး ။ ကၽြန္ေတာ္တို႔ ဟာ သခ်ာၤကို အဆင္႔တစ္ဆင္႔ခ်င္းဆီမွာ တိက်တဲ႔ အေၾကာင္းျပခ်က္ေတြရွာေဖြၿပီး ေဖာ္ျမဴလာေတြထုတ္ခဲ႔ၾကတယ္ ။ အဲ ဒီထုတ္ခဲ႔တဲ႔ ေဖာ္ျမဴလာေတြအတိုင္း လက္ေတြ႔နယ္ပယ္မွာ အသံုးခ်ခဲ႔ၾကတယ္ ။
ဥပမာ အေနနဲ႔ ခဲတံတစ္ခုနဲ႔ စာရြက္ပိုင္းတစ္ခုေပၚမွာ မ်ဥ္းတစ္ေၾကာင္းဆြဲလိုက္ပါ ။ အဲဒီစာရြက္ဟာ တစ္လက္မေလာက္ပဲရွည္ခ်င္ရွည္ပါလိမ္႔မယ္ ။ ၿပီးေတာ႔ မ်ဥ္ရဲ့ အစြန္းတစ္ဖက္ကို 0 လု႔ိ မွတ္ၿပီး ၊ ေနာင္စြန္းတစ္ဖက္ကို 1 လု႔ိ မွတ္လိုက္ပါ ။ အဲဒီမ်ဥ္းေၾကာင္းေလးရဲ့ အပိုင္းေလး ဟာ [0,1] ပါ။ ဒါေပမဲ႔ ေနာက္ ထပ္ မ်ဥး္ကိုအဆံုးဆမရွိ ဆက္ဆြဲနိုင္ပါေသးတယ္ ။အဆံုးအဆမရွိတဲ႔ အမွတ္ေတြလည္းရွိေနပါေသးတယ္ ။ ဒါေပမဲ႔ စာရြက္ဟာ ကန္႔သတ္ခ်က္ျဖစ္ေနပါတယ္ ။ မ်က္ျမင္ကမၻာ ဟာလည္း စာရြက္အပိုင္းလိုပါပဲ ။ ကၽြန္ေတာ္တို႔ အျမင္ေတြကန္႔သတ္မွဳေတြ ရွိေနေပမဲ႔ အေတြးအေခၚမ်ဥ္းေတြေတာ႔ ဆက္ဆြဲ လို႔ရေနပါေသးတယ္ ။ ဒါေပ မဲ႔ အဲဒီအေတြးအေခၚမ်ဥ္းေတြကို လက္ေတြ႔ (ျမက္ျမင္ကိုယ္ေတြ႔) ကမၻာမွာ ခ်ျပလို႔ရနိုင္ေအာင္ ၊ ရွင္းျပလို႔ရနိုင္ေအာင္ ေပါင္းကူးေပးမဲ႔အရာ တစ္ခု ရွိေနပါတယ္ ။ အဲဒါကေတာ႔ ကၽြန္ေတာ္တို႔ သင္ၾကားခဲ႔ရတဲ႔ ကာကုလပ္စ္ ဆိုတဲ႔ အရာႀကီးပါပဲ ။
ကနဦးအစ ကကၽြန္ေတာ္ေျပာခဲ႔သလိုပါပဲ ။ ကဲကုလပ္စ္ ဟာ ဒါႀကီးပါလို႔ လက္ဆုပ္လက္ကိုင္ ျပလို႔ရတဲ႔အရာ မဟုတ္ပါဘူး ။ tutorial ေတြ ၊ training course ေတြလို ဒါ ၿပီးရင္ဒါလုပ္ဆိုတဲ႔ ပညာရပ္မ်ိဳးလည္းမဟုတ္ပါဘူး ။ဆက္စပ္ ျဖစ္ေပၚလာတဲ႔ ေတြးေခၚမွဳမ်ိဳးပါ ။ ဒါေၾကာင္႔ ကဲကုလပ္စ္ မေပၚခင္ ကစလို႔ သခ်ာၤသမိုင္းအနည္းအက်ဥ္းကို အရွည္ႀကီးေျပာျပခဲ႔တာပါ ။ အေပၚကစာေတြ ဖတ္ၿပီးတဲ႔ခါ ကဲကုလပ္စ္ဟာ ဘယ္လိုအရာလည္းအနည္းငယ္သေဘာေပါက္မယ္ထင္ပါတယ္ ။ (ကၽြန္ေတာ္႔စာအေရးသားကိုကၽြန္ေတာ္သိလု႔ိ နည္းနည္းနားလည္လိမ္႔မယ္ထင္တယ္လို႔ေျပာတာေနာ္ … စာဖတ္သူကိုအထင္ေသးလို႔မဟုတ္ပါ … း) …. )
ကဲကုလပ္စ္ ရဲ့ လက္တင္ဘာသာ အဓိပၸါယ္ကေတာ႔ ေရတြက္ရမွာသံုးတဲ႔ ေက်ာက္တံုးအေသးစားေလးလို႔ အဓိပၸါယ္ရပါတယ္ ။ ကဲကုလပ္စ္မွာ Limit , differentiate,integral,infinite စတဲ႔အပိုင္းေတြ ပါဝင္ပါတယ္ ။ သိုေပမဲ႔ အဓိက သေဘာတရားကေတာ႔ differential , integral တို႔ပါပဲ ။ differential ရဲ့ သေဘာကေတာ႔ ကၽြန္ေတာ္တို႔ အေတြးအေခၚေတြ ကို တကယ္႔ လက္ေတြ႔နယ္ပယ္နဲ႔ ဆက္စပ္နိုင္ဖို႔ ခ်ံဳ႕ ယူလိုက္တာပါ ။ ၿပီးတဲ႔ အခါမွာ ကၽြန္ေတာ္တုိ႔ အငယ္ဆံုးတန္ဖိုးေတြရလာမယ္ ။ ေဖာ္ျမဴလာေတြ ၊ အီေကြးရွင္းေတြ အျဖစ္ထုတ္ၾကမယ္ ။ အဲဒီရလာတဲ႔ေဖာ္ျမဴလာေတြ အီေကြးရွင္းေတြ ကို တခါ ျပန္ၿပီးေျပာင္းျပန္ေပါ႔ ျပန္ခ်ဲ႕ ၾကည့္ဖို႔ က်ေတာ႔ အင္တီဂရိတ္ကိုသံုးပါတယ္ ။ ဒါေၾကာင္႔ ကၽြန္ေတာ္ လိုလူၿပိန္း အေနနဲ႔ မွတ္သားမယ္ဆိုရင္ေတာ႔ differentiate ဆိုတာခ်ံဳ႔ၾကည့္တာ ၊ integrate ဆိုတာျပန္ခ်ဲ႔ ၾကည့္တာ ပါပဲ (တကယ္ တိတိက်က် ေလ႔လာမယ္ဆိုရင္ေတာ႔ ဒီထက္ပိုနိုင္ပါတယ္ ၊ ကၽြန္ေတာ္ ကသေဘာတရားကိုပဲ ဆိုလိုတာပါ ) ။
ကဲကုလပ္စ္ ကိုဘယ္ေနရာေတြမွာ သံုးလဲ ။ သေဘာတရား ကေတာ႔ သိပၸံ ပညာ ရဲ့ နယ္ပယ္စံုမွာ သံုးတယ္လို႔ ဆိုရပါ႔မယ္ ။ ဘာရည္ရြယ္ခ်က္နဲ႔ သံုးလဲဆိုေတာ႔ အေပၚမွာ ေျပာခဲ႔သလိုပါပဲ ကၽြန္ေတာ္တို႔ မ်က္ျမင္ မေတြ႔ နိုင္တဲ႔ အရာေတြကို လက္ေတြ ျပသဖို႔ နဲ႔ ကၽြန္ေတာ္တို႔ လက္ေတြ႔ မႀကံဳရေသးတဲ႔ အေျခေနေတြကို တိက်မွန္ကန္တဲ႔ နည္းလမ္းေတြ နဲ႔ ႀကိဳတင္ခန္႔မွန္းနိုင္ဖို႔ပါပဲ ။ ဥပမာ ေပါ႔ ကားတစ္စီးက တစ္မိနစ္ကို ၁၀ မိုင္ ခရီးေရာက္တယ္လို႔ ဆိုပါေတာ႔၊ မိုင္ ၁၀၀ ဆို အခ်ိန္ဘယ္ေလာက္နဲ႔ ေမာင္းနိုင္မလဲ ကၽြန္ေတာ္တို႔ ႀကိဳတင္ခန္႔မွန္းလို႔ရပါၿပီ ။ အလားတူ ကဲကုလပ္စ္ သေဘာတရား ေတြ နဲ႔ ပဲ ကမၻာႀကီးဟာ speed ဘယ္ေလာက္နဲ႔ ေနကိုလွည့္ပတ္ေနသလဲ ၊ ကမၻာ ရဲ့ ေနကိုပတ္တဲ႔ ပတ္လမ္းဟာ ဘယ္ေလာက္ အတိုင္းတာရွိသလဲဆိုတာကို ကၽြန္ေတာ္တို႔လူေတြသိနိုင္ခဲ႔တာပါ ။ ကမၻာ ႀကီးအျပင္ဘက္ကို လူေတြ ထြက္ၿပီး ၊ ကမၻာႀကီး ပတ္တဲ႔လမ္းအတိုင္ း ေနကို ပတ္ခ်ာလွည့္တိုင္းလို႔ သိခဲ႔ၾကတာမဟုတ္ဘူး ။ ေနာက္ Control systems ေတြ တည္ေဆာက္ရာ ၊ အာကာသယာဥ္ေတြ ၊ ေလယာဥ္ေတြ တည္ေဆာက္ရာ မွာ လူကိုယ္တိုင္လိုက္ပါ စမ္းသပ္မယ္ဆုိရင္ မလိုအပ္ပဲ လူေတြ အသက္ေတြဆံုးရွံုးမယ္ ၊ အရင္းႏွီး မ်ားႀကီးေပးဆပ္ရနိုင္တယ္ ။ အဲဒီ အခ်ိန္ေတြမွာ ဘာလုပ္လဲ ကဲကုလပ္ ကိုသံုးၿပီး mathematical model ေတြ တည္ေဆာက္တယ္ ၊ ကြန္ျပဴတာနဲ႔ visualized လုပ္ၿပီးေတာ႔ simulation ေတြ လုပ္ၾကည့္မယ္ ။ တိက် ၊ မွန္ကန္တဲ႔ရလဒ္ေတြထြက္လာတဲ႔အခါမွ လက္ေတြ႔မွာတည္ေဆာက္တယ္ ။ ဒါဆိုရင္ ဆံုးရွံဳးမွုလည္းနည္းမယ္ ၊ ျမန္လည္းျမန္ဆန္မယ္ ။ ဒါေတြ ဟာ ကဲကုလပ္စ္ ကေနရလာတဲ႔ အက်ိဳးေက်းဇူးေတြပဲျဖစ္ပါတယ္ ။
ကဲဗ်ာ ဒီေလာက္ဆိုရင္ေတာ႔ ကၽြန္ေတာ္တို႔ေက်ာင္းသားေတြ ၊ ဗဟုသုတရွာေဖြသူေတြအေနနဲ႔ ကဲကုလပ္စ္ကို ဘာေၾကာင္႔ သင္ေနၾကရလဲ ၊ ေလ႔လာေနၾကရလဲ ၊ ကဲကုလပ္စ္ ဆိုတာဘာလဲ ၊ ကဲကုလပ္စ္ရဲ့ သေဘာသဘာဝကေရာဘာလဲ ၊ ကဲကုလပ္စ္ကို ဘယ္ေနရာေတြမွာအသံုးခ်လဲ ဆိုတာ ဗဟုသုတရၾကလိမ္႔မယ္လို႔ထင္ပါတယ္ ။ ကၽြန္ေတာ္ဟာ သခ်ာၤပညာရွင္မဟုတ္တဲ႔အတြက္ ကၽြန္ေတာ႔ေရးသားမွဳမွာ အမွားေတြပါေကာင္းပါနိုင္ပါတယ္ ။ ဒါေပမဲ႔ ပညာရပ္တစ္ခုအတြက္ ဗဟုသုတေလး ရသြားတယ္ဆိုရင္ ကၽြန္ေတာ္ေရးသားရက်ိဳးနပ္တယ္လို႔ခံယူပါတယ္ ။ ကဲကုလပ္ကိုလက္ေတြ႔ အသံုးခ်မွု နဲ႔ ဆက္စပ္တာေလးေတြေတာ႔ အခ်ိန္ရရင္ ထပ္ေရးသားပါဦးမယ္ ။
by ၇ုပ္ဆိုး
ကိုးကား
http://wikimyanmar.co.cc/wiki/index....80%95%E1%80%B9
http://www.math.vanderbilt.edu/~sche.../whystudy.html
http://en.wikipedia.org/wiki/Calculus
http://www.calculus.org/
ကၽြန္ေတာ္တို႔ေက်ာင္းသူေက်ာင္းသားေတြ ဟာ ငယ္ငယ္ေလးတည္းက ပညာရပ္ေတြ သင္ၾကားခဲ႔ၾကရတယ္ ။ တခ်ိဳ႔ပညာရပ္ေတြ ၊ သီအိုရီေတြက လက္ေတြ႔ မွာအသံုးခ်နိုင္တယ္ ။ တခ်ိဳ႕ ပညာရပ္ေတြ သီအိုရီေတြ ကေတာ႔ ေတြ႔ျမင္ေနရတဲ႔ ပတ္ဝန္းက်င္နဲ႔ဆက္စပ္ၾကည့္လို႔မရဘူး ။ အဲဒီခ်ိန္ဆိုရင္ ကၽြန္ေတာ္တို႔ အမ်ားဆံုး သိခ်င္တဲ႔ေမးခြန္းက ကၽြန္ေတာ္တို႔ဘာေၾကာင္႔ ဒီပညာရပ္ကိုေလ႔လာရတာပါလဲ ဆိုတဲ႔ေမးခြန္းပါပဲ ။ ဆရာသမားေတြကိုေမးၾကတယ္ ။ ကၽြန္ေတာ္တို႔လိုခ်င္တဲ႔အေျဖရသည္လည္းရွိတယ္ မရသည္လည္းရွိတယ္ ။ အဲဒီေတာ႔ကၽြန္ေတာ္တို႔စိတ္ထဲမွာထင္လာတယ္ ။ အဲဒီပညာရပ္ေတြကို စာေမးပြဲအတြက္တင္ပဲ ကၽြန္ေတာ္တို႔ေလ႔လာၾကတာလား။ ဒါမွမဟုတ္ သင္ရိုးညႊန္းတမ္း ကျပဌာန္း ေပးလိုက္လို႔ မ်ား ကၽြန္ေတာ္တို႔ မျဖစ္မေနသင္ေနၾကရတာလား ။ နက္နက္ရွိဳင္းရွိဳင္းစဥ္းစားၾကည့္မယ္ဆိုရင္ ကၽြန္ေတာ္တို႔ ထပ္ကာထပ္ကာ ေလ႔လာသင္ယူေနခဲ႔ရတဲ႔ အေၾကာင္းရာေတြကတကယ္တမ္း လက္ေတြ႔ မွာေရာ အသံုးခ်နိုင္ရဲ့လား။ တခ်ဳိ႔ တခ်ိဳ႕ ေသာ ေက်ာင္းသားေတြကေတာ႔ သူတို႔ရဲ့ အလုပ္ခြင္ျဖစ္တဲ႔ ရူပေဗဒဆုိင္ရာေတြ ၊ ဓာတုေဗဒ ဆုိင္ရာေတြ ၊ စတဲ႔သက္ဆိုင္ရာနယ္ပယ္ေတြမွာ calculus သင္ခန္းစာေတြကို ကို အသံုးခ်ေနၾကပါတယ္ ။ ဒါေပမဲ႔ အားလံုး နီးပါးဟာ ဘာေၾကာင္႔ ဒီပညာရပ္ကို ေလ႔လာတာလဲဆိုတာ ကို သိရွိၿပီးမွ အသံုးခ်ေနၾကတာမဟုတ္ပါဘူး ။ အားလံုးအတြက္လည္း ကကုလပ္စ္ အေၾကာင္းသက္ေသျပဖို႔ မလိုအပ္ပါဘူး ။ ဘာေၾကာင္႔ လဲဆိုေတာ႔ ဒီအလုပ္ဟာ သခ်ာၤပညာရွင္ ေတြသာလွ်င္ လုပ္ရမဲ႔အလုပ္လို႔ ယံုၾကည္ေနၾကလို႔ပါပဲ ။ ဒါဆိုရင္ကၽြန္ေတာ္တို႔က ဘာလို႔မ်ား ကဲကုလပ္စ္ အေၾကာင္းေတြကို ေလ႔လာေနၾကတာလဲ ။
တကယ္ေတာ႔ ကဲကုလပ္စ္ ဟာ အလုပ္တစ္ခုကိုမဝင္ခင္မွာ အလုပ္ရဖို႔အတြက္ ႀကိဳတင္ျပင္ဆင္ တဲ႔ training course တစ္ခုမဟုတ္ပါဘူး ။ ကြန္ပ်ဴတာဘာသာရပ္ေတြလို ဒီဟာကို ဒီလိုေလးလုပ္ ဆိုၿပီးလိုက္လုပ္ၿပီးတက္ေျမာက္သြားတဲ႔ အရာမဟုတ္ဘူး ။ ဒါဝင္ ၊ မာ႔ခ္ ၊ ေဗာ္လ္တိုင္းရား ၊ ေဒါ႔စေတာ႔ရဗ္စကီး တို႔ လို အေတြးအေခၚပိုင္းနဲ႔ဆက္စပ္ၿပီး ေလ႔လာျခင္းတစ္မ်ိဳးပါပဲ ။ ဒီ အေတြးအေခၚ ေတြဟာကၽြန္ေတာ္တို႔ လူေနမွုဘဝေတြရဲ့ အျခခံအစိတ္အပိုင္းေတြ ၊ ကၽြန္ေတာ္တို႔ ကမၻာႀကီးကို ဘယ္လိုယူဆပံုေဖာ္သလဲ ၊ ကမၻာ ေပၚ က ကၽြန္ေတာ္တို႔ရဲ့ ေနရာေတြကိုဘယ္လို သိရွိနိုင္မလဲဆိုတဲ႔ ေမးခြန္းေတြနဲ႔ဆက္စပ္ေနပါတယ္ ။ ကၽြန္ေတာ္တို႔ဟာ ကာ႔ကုလပ္စ္ရဲ့ သေဘာအမွန္ကိုသိနိုင္ဖို႔ဆိုရင္ ကဲ႔ကုလပ္စ္ရဲ့ သမိုင္းေၾကာင္းကိုလည္းထည့္သြင္းေလ႔လာဖို႔လိုပါမယ္ ။ ၿပီးတဲ႔အခါမွာ ကာ႔ကုလပ္စ္မေပၚခင္ကကမၻာႀကီးရဲ့အေျခအေနနဲ႔ကာ႔ကုလပ္စ္ေပၚၿပိးေနာက္ကမၻာႀကီးရဲ့အေျခေနေတြကိုႏွိုင္းယွဥ္သံုးသပ္ရပါမယ္ ။ အဲဒီအခါ မွသာ ကၽြန္ေတာ္တို႔ ကဲကုလပ္စ္ ဘယ္ကျဖစ္လာသလဲ ။ ကၽြန္ေတာ္တို႔ ေက်ာင္းသူေက်ာင္းသားေတြ ကဲကုလပ္စ္ကို ဘာေၾကာင္႔ေလ႔လာဖို႔လိုသလဲဆိုတာ သေဘာေပါက္လာမွာျဖစ္ပါတယ္ ။
ကဲကုလပ္စ္ ဟာ သခ်ာၤရဲ့ အစိတ္အပိုင္းဆိုေတာ႔ သခ်ာၤအေၾကာင္းစ ေျပာၾကည့္ရေအာင္ ။ သခ်ာၤရဲ့ အစက ကုန္သြယ္မွဳကလိုဆိုရလိမ္႔မယ္ ။ ဥပမာ ႏြားတစ္ေကာင္ဟာ ဆိတ္ သံုးေကာင္တန္ဖိုးရွိတယ္ဆိုပါေတာ႔ ။ ႏြားေလး ေကာင္ဆိုရင္ ဆိတ္ ဘယ္ႏွေကာင္စာ နဲ႔ ညီမွ် မလဲ ။ ဒီသေဘာတရားဟာ သခ်ာၤရဲ့ အေျခခံ ေပါင္းႏွဳတ္ေျမွာက္စား နဲ႔ လက္ေတြ႔ နယ္ပယ္နဲ႔ ဆက္စပ္မွဳပါ ။ ဂ်ီၾသေမႀတီ ဆိုရင္လည္း အမွတ္ေတြ ၊ မ်ဥ္းေတြ ၊ ေထာင္႔ ေတြ စတဲ႔ အေၾကာင္းရာေတြနဲ႔ တကယ္႔လက္ေတြ႔ဘဝက အေဆာက္ဦးေတြေဆာက္ရာ မွာ မ်ားစြာအသံုး ဝင္ခဲ႔ၾကပါတယ္ ။ ဒါဟာဘာကိုျပသလဲဆိုေတာ႔ လူေတြ ရဲ့ ပတ္ဝန္းက်င္သဘာဝ မွာျဖစ္ပ်က္ ျမင္ေတြ႔ ေနရတဲ႔ အရာေတြကေနၿပီးသခ်ာၤ နည္းစနစ္ေတြဟာ ျဖစ္ေပၚလာခဲ႔ၾကတယ္ ၊ အသံုးဝင္ ခဲ႔ၾကတယ္ ၊ ဆက္လက္ က်ယ္ျပန္႔လာခဲ႔ၾကတယ္ ဆိုတာကိုေျပာျပေနတာျဖစ္ပါတယ္ ။
ေရွးေဟာင္း ဂရိပညာရွင္ေတြဟာ အေတြးေခၚမွာ အရမ္းကိုထက္ျမက္ခဲ႔ၾကပါတယ္ ၊ ဒါေပမဲ႔ စမ္းသပ္အသံုးခ်မွုမွာေတာ႔အားနည္းခဲ႔ၾကတယ္ ။ ဥပမာ အေနနဲ႔ ျပရမယ္ဆိုရင္ အရစၥတိုလ္တယ္ ဟာ ငွက္ေမႊးထက္ေက်ာက္တံုး က ပိုၿပီးျမန္ျမန္က်တယ္ဆုိတာကိုေလ႔လာေတြ႔ရွိခဲ႔တယ္ ။ ၿပီးတဲ႔ ခါမွာ သူ ေကာက္ခ်က္ခ်လိုက္တာက ေလးတဲ႔အရာ ေတြဟာ ေပါ႔ပါးတဲ႔အရာေတြထက္ ေအာက္ကိုျမန္ျမန္က်တယ္ဆိုတာပါပဲ ။ စမ္းသပ္အသံုးခ်မွဳ မရွိပဲ အေတြးေခၚကေနဆင္းသက္လာတဲ႔ အရစၥတိုလ္တယ္ ရဲ့ အဲဒီအျမင္ဟာ Air resistance ကို ရွာေဖြ မေတြ႔ခင္ ခ်ိန္ထိ ရာစုႏွစ္တိုင္ေအာင္တည္တ႔ံေနခဲ႔တယ္ ။ အခ်ိန္အတိုင္းတာတစ္ခုထိ မွန္ကန္ေနတယ္လို႔ ဆိုနိုင္ပါတယ္ ။ ဒါေပမဲ႔ လက္ေတြ႔စမ္းသပ္ အသံုးခ်မွဳရဲ့ေနာက္ကြယ္မွာေတာ႔ သူ႔အယူအဆေမွးမွိန္ခဲ႔ရတယ္ ။
ေနာက္ထပ္ ကဲကုလပ္စ္ ရဲ့ ပံုျပင္ ဆန္ဆန္ အစိတ္ပိုင္းကေတာ႔ ကာ႔ကုလပ္စ္ဟာ နကၡတ္ေဗဒႏွင္႔ အတူျဖစ္ေပၚလာတယ္လို႔ဆိုပါတယ္ ။ လူေတြဟာ လူေတြေရာက္ရွိေနရာ ေနရာ နဲ႔ လူေတြထိန္းခ်ဳပ္မွဳက လြတ္ကင္းေနတဲ႔ အေျခေနေတြမွာ ေရွ့ျဖစ္လာမဲ႔ အရာေတြကို ႀကိဳတင္ေဟာကိန္းထုတ္နိုင္ဖို႔ ႀကိဳးစားခဲ႔ၾကတယ္ ။ အေမွာင္နဲ႔ ေအးစက္မွဳကိုေၾကာက္တဲ႔လူေတြကိုအေမွာင္နဲ႔အေအးကိုမေၾကာက္ပါနဲ႔လို႔ေျပာမဲ႔အစား၊ေႏြးေထြးတဲ႔အခါလည္းတလွည့္ျပန္လာဦးမွာပါ ။ အရာရာဟာစက္ဝိုင္းပမာပါ ။ ျဖစ္ျပန္ပ်က္ျပန္ ေလာကဓံေပါ႔ ၊ အဆိုးေတြလည္းရွိသလို အေကာင္းေတြလည္းရွိနိုင္ပါေသးတယ္ ။ စတဲ႔အားေပးမွုမ်ိဳးကိုေျပာသင္႔တယ္ ၊ အဲလုိ အားေပးမွဳ မ်ိဳးကလည္း အက်ိဳးေက်းဇူးပုိမ်ားေစတယ္လို႔လူေတြကေတြးေခၚခဲ႔ၾကတယ္ ။
ကမၻာႀကီးဟာ စၾကၤာဝဠာရဲ့အလယ္မွာရွိေနတယ္ ။ ေန႔တစ္ေန႔မွာ ဆိုရင္ ေနမင္းႀကီး က အေရွ့ ကေန ထြက္ၿပီးေတာ႔ အေနာက္ဘက္မွာျပန္ဝင္သြားတယ္ ။ ညတစ္ည မွာဆိုရင္ ၾကယ္အစုေဝးေတြက အေရွ့ကထြက္ၿပီး အေနာက္မွာျပန္ဝင္သြားတယ္ ။ ၾကယ္ေတြဟာ တစ္ခုနဲ႔ တစ္ခု ဆက္ႏႊယ္ၿပီးတည္ရွိေနၾကတယ္ ။ ၿပီးေတာ႔ အဲဒီ ၾကယ္ေတြ ၊ ၿဂိဳလ္ေတြရဲ့ ေရြ႔ လ်ားမွုဟာ တစ္သမတ္တည္းရွိေနတာမဟုတ္ပဲ ေရာေထြးေနတယ္ ။ နကၡတ္ေဗဒ ပညာရွင္ေတြဟာ ၿဂိဳလ္ေတြရဲ့ ေရြ႕လ်ားမွု ကိုေသခ်ာမွတ္သားၿပီးေတာ႔ ေနာက္လာမဲ႔ အနာဂါတ္မွာအဲဒီၿဂိဳလ္ဟာဘယ္ပံုစံေရြ႕လ်ားမလဲဆိုတာ ခန႔္မွန္းၾကတယ္ ၊ ေရြ႕လ်ားမွဳေျပာင္းလဲျခင္းနဲ႔ပက္သက္ၿပီး လူေတြ အေပၚမွာဘယ္လိုသက္ေရာက္မွုရွိလဲ ဆိုတာလည္း မွတ္သားၾကတယ္ ။
၁၅၄၃ ခုႏွစ္မွာေတာ႔ ေကာ႔ပါးနီးကပ္စ္ ဟာ ၿဂိဳလ္ေတြက ကမၻာကိုလွည့္တာမဟုတ္ပဲ၊ ေနကိုလွည့္ ေနတာျဖစ္တယ္ ဆိုတဲ႔ သူ႔ရဲ့ ေလ႔လာခ်က္ ကိုအသံုးျပဳၿပီး ၿဂိဳလ္ေတြရဲ့ ေရြးလ်ားမွဳကို ရိုးရွင္းစြာ ရွင္းျပနိုင္ခဲ႔တယ္ ။ ၿပီးေတာ႔ ကမၻာႀကီးကိုယ္တိုင္ကလည္းပဲ ေနကိုလွည့္ေနတာလို႔ေျပာခဲ႔တယ္ ။ သူ ရွင္းျပခဲ႔တဲ႔ ၿဂိဳလ္ေတြရဲ့ ပတ္လမ္းဟာ စက္ဝိုင္းပံု နီးနီး ျဖစ္ပါတယ္ ။ သူ႔အယူအဆကို church ေက်ာင္းက လက္မခံခဲ႔ဘူး ။ ဘာလို႔လဲဆိုေတာ႔ ဘုရားသခင္ဖန္းဆင္းတဲ႔ ကမၻာေျမဟာ တျခားအရာေတြထက္ အေရးပို မပါသလိုျဖစ္ေနလို႔ ပါ ပဲ ။ အဲဒါေၾကာင္႔လဲေကာ႔ပါးနီးကပ္စ္ ကို church ေက်ာင္းကေနျပစ္ဒဏ္ေပးခဲ႔ပါတယ္ ။
၁၅၈၀-၁၅၉၇ ႏွစ္ေတြမွာေတာ႔ ဘရာ႔ဟဲ ႏွင္႔ သူ႔လက္ေထာက္ ကပ္ပလာ တို႔ဟာ ပိုမိုတိက်တဲ႔ ၿဂိဳလ္ေတြေလ႔လာမွဳ အေျမာက္အမ်ားျပဳလုပ္ခဲ႔ၾကတယ္ ။ ကပ္ပလာ ဟာ အဲဒီေလ႔လာခ်က္ေတြကိုအေျခခံၿပီးေတာ႔ ၁၅၉၆ ခုႏွစ္မွာ ေကာ႔ပါးနီးကပ္စ္ ရဲ့ အယူအဆျပင္ဆင္ခ်က္ကို ထုတ္ျပန္ခဲ႔တယ္ ။ ကပ္ပလာ ဟာ ၿဂိဳလ္ေတြရဲ့ ပတ္လမ္းဟာစက္ဝိုင္းပံုမဟုတ္ပဲ ဘဲဥပံုလမ္းေၾကာင္း (ellipses) ျဖစ္တယ္ဆိုတာျပသခဲ႔တယ္ ။ ေျမာက္မ်ားစြာေသာ ၿဂိဳလ္ေတြေရြ႕လ်ားမွဳနဲ႔ပက္သက္ၿပီး ရိုးရွင္းၿပီး တိက် တဲ႔ နိယာမ ၃ ခုကို ကပ္ပလာ က ထုတ္ျပန္ခဲ႔တယ္ ။
(၁) ေနကိုဦးတည္လည္ပတ္မွဳနဲ႔အတူ ၿဂိဳလ္ေတြရဲ့ပတ္လမ္းဟာ ဘဲဥပံုျဖစ္တယ္ ။
(၂) ေနႏွင္႔ ၿဂိဳလ္ ေတြၾကားမွာ ရွိတဲ႔ အကြာေဝးကို ဆန္႔ထုတ္ဖို႔ အတြက္ေျပာင္းလဲတဲ႔ ၿဂိဳလ္ ရဲ့ အလ်င္ ဟာ ပံုမွန္ႏွဳန္း(ကိန္းေသႏွဳန္း) နဲ႔ တိုးတိုးသြားတယ္ ။
(၃) ပတ္လမ္းအတြက္ၾကာခ်ိန္ ႏွစ္ဆ ဟာ ေနနဲ႔ ၿဂိဳလ္ရဲ့ ၾကားက ပ်မ္းမွ်အကြားေဝး ၃ ဆ နဲ႔ အခ်ိဳးညီတယ္။
ဆိုတဲ႔ နိယာမ ၃ ခုျဖစ္ပါတယ္ ။
၁၆၀၉ ခုႏွစ္မွာေတာ႔ ဂယ္လီလီယို ဟာ စပိုင္ဂလက္စ္(spyglass) ကိုတီထြင္ခဲ႔တယ္ ။ အဲဒီအခ်ိန္တုန္းကေတာ႔ လူသိမ်ားတဲ႔ ပစ္စည္းတစ္ခုေပါ႔ ။ စပိုက္ဂလက္စ္ကို တယ္လီစကုတ္ အေနနဲ႔ အသံုးခ်ၿပီး ေကာင္းကင္ဘံုကုိ ေလ႔လာခဲ႔ၾကတယ္ ။ ဂယ္လီလီယို ဟာ သာမန္မ်က္စိေတြ နဲ႔ မျမင္ေတြ႔ နိုင္တဲ႔ ေျမာက္မ်ားစြာေသာ ေန ၊ လ ၊ ၿဂိဳလ္ နဲ႔ နကၡတ္ ေတြကို ေလ႔လာခဲ႔တယ္ ။ အဲလို သူ ေလ႔လာတဲ႔အခါမွာ ဂ်ဴပီတာၿဂိဳလ္ရဲ့ ၿဂိဳလ္ရံလဟာ ဂ်ဴပီတာၿဂိဳလ္ကို လွည့္ပတ္ ေနတာ သူရွင္းရွင္းလင္းလင္းေတြ႔ခဲ႔ရတယ္ ။ ဒီအခ်က္ ဟာ ကိုပါးနီးကပ္စ္ ထုတ္ေဖာ္ခဲ႔တဲ႔ အရာတိုင္းက ကမၻာကို ခ်ည္းပဲ လွည့္ပတ္ေနတာမဟုတ္ဘူးဆိုတဲ႔ အယူအဆရဲ့ ရိုးရွင္းခိုင္မာတဲ႔ အေထာက္ထား ျဖစ္တယ္ ။ ကိုပါးနီးကပ္စ္ တုန္းကလိုပဲ church ေက်ာင္း ကေနၿပီးေတာ႔ ဂယ္လီလီယို ကိုပစ္ဒဏ္ေပးခဲ႔တယ္ ။ ဒါေပမဲ႔ သူ႔ရဲ့အယူအဆကေတာ႔ တစ္ကမၻာ လံုး မွာရပ္တန္႔လို႔ မရေတာ႔ေလာက္ေအာင္ တစ္ႀကိမ္တည္းျပန္႔ႏွံ႔သြားခဲ႔တယ္။
ဂယ္လီလီယို ဟာ ကမၻာဆြဲအားနဲ႔ ပက္သက္ၿပီးေတာ႔လည္း တုိင္းတာနိုင္ဖို႔ စမ္းသပ္ခဲ႔တယ္။ အရစၥတိုတယ္လ္ ရဲ့ ပိုေလးတဲ႔အရာဝထၳဳက ေပါ႔တဲ႔ အရာထက္ ေအာက္ကိုျမန္ျမန္က်တယ္ ဆိုတဲ႔ အယူအဆကိုမွားယြင္းေၾကာင္း လက္ေတြ႔ျပသခဲ႔တယ္။ သူဟာ အရြယ္စားမတူညီတဲ႔ ေဘာလံုးေလးေတြကို ေလွ်ာေဇာက္မွာလိွမ္႔ခ်ၿပီးေတာ႔ ေအာက္ ကိုက်ဖုိ႔ ၾကာတဲ႔ အခ်ိန္ကိုေသခ်ာ မွတ္သားျခင္း ျဖင္႔ စမ္းသပ္ခဲ႔တယ္ ။ ေနာက္ထပ္ ၁၀ ေပါင္ဆီေလးတဲ႔ အရာဝထၳဳ ၃ ခုကို ေမွ်ာ္စင္ေပၚကေန ပစ္ခ်လိုက္တဲ႔အခါမွာ အားလံုးက ေျမႀကီးေပၚကို တခ်ိန္တည္းမွာက်ေရာက္သြားၾကတယ္ ။ ထပ္ၿပီးေတာ႔ အရာဝထၳဳ ၃ ခုတည္းက ၂ ခုကို ႀကိဳး တိုတို တေခ်ာင္းနဲ႔ ဆက္သြယ္ခ်ည္ေႏွာင္ၿပီး ပစ္ခ်လိုက္တဲ႔အခါမွာလည္း အရာဝထၳဳေတြဟာ ေျမႀကီးေပၚကိုအတူတူ က်သြားၾကတယ္ ။ ေနာက္ တတိယအႀကိမ္မွာေတာ႔ ႀကဳိးအစား စူပါဂလူး ကိုသံုးၿပီးေတာ႔ အရာဝထၳဳ ၂ ခုကို ေကာ္နဲ႔ပူးကပ္ၿပီးေတာ႔ ပစ္ခ်လိုက္တဲ႔အခါမွာ နဂို ၁၀ ေပါင္ရွိတဲ႔ အရာဝထၳဳ ၃ ခု ဟာ ေျမႀကီးေပၚကိုအတူတူက်သြားၾကတယ္ ။ ဒါေပမဲ႔ ေကာ္ေတြေျခာက္သြားၿပီျဖစ္လို႔ နဂို ၁၀ ေပါင္ စီရွိေနတဲ႔ အရာဝထၳဳ ၃ ခုကေနၿပီးေတာ႔ ေပါင္၂၀ ေလးတဲ႔အရာဝထၳဳတစ္ခု နဲ႔ ၁၀ ေပါင္ေလးတဲ႔အရာဝထၳဳ တစ္ခုျဖစ္ေနတာကို ေတြ႔ခဲ႔ရတယ္ ။ အဲဒါေၾကာင္႔ပဲ ဂယ္လီလီယို ဟာ အရစၥတိုတယ္လ္ ေျပာခဲ႔တဲ႔ ပုိေလး ေလး ေအာက္ကိုျမန္ျမန္က်ေလဆိုတဲ႔ ယူဆခ်က္ကုိ မွားယြင္းေၾကာင္း ေျပာခဲ႔တာပဲျဖစ္ပါတယ္ ။
အဲလိုနဲ႔ပဲ ကာကုလပ္ရယ္လု႔ိျဖစ္ေပၚလာမဲ႔ အေျခခံအေတြးေခၚေတြဟာရာစုႏွစ္မ်ားစြာ လည္ပတ္ေနခဲ႔တယ္ ။ ဒါေပမဲ႔ အဲဒီ အယူအဆေတြကို ထုတ္ျပ မဲ႔ လူ ၂ ေယာက္ထက္ၿပီးထြက္ေပၚလာခဲ႔တယ္ ။ အဲဒီလူေတြကေတာ႔ နယူတန္ (Newton) နဲ႔ လစ္ဘနစ္စ္ (Leibniz) တို႔ပါပဲ။ သူတို႔ ၂ ေယာက္ဟာ ေခတ္ကာလတစ္ခုတည္းမွာပဲ တစ္ဦးခ်င္းစီ တစ္ေနရာစီမွာ ကာ႔ကုလပ္စ္ရဲ့ အေျခခံ သီအိုရီ ေတြကို ေလ႔လာခဲ႔တယ္ ။ နယူတန္ နဲ႔ လစ္ဘနစ္စ္ တို႔ဟာ ကာကုလပ္စ္ကုိ ၂ ေယာက္စလံုးတီထြင္ခဲ႔ၾကတယ္ဆိုေပမဲ႔ နယူတန္ဟာပိုၿပီးေတာ႔ လုပ္ေဆာင္နိုင္ခဲ႔တယ္ ။ Derivative ဆိုတာ ေျပာင္းလဲတဲ႔ႏွုန္းပါပဲ ။ ကမၻာေပၚမွာျဖစ္ျဖစ္ သမွ် ၊ ရွိရွိသမွ် အရာအားလံုးဟာ အခ်ိန္တိုင္းနဲ႔ အမွ် ေျပာင္းလဲေနပါတယ္ ။ ဒါေၾကာင္႔လဲ derivatives ဟာမ်ားစြာအသံုးဝင္လာပါတယ္ ။ ၁၆၈၇ ခုႏွစ္မွာေတာ႔ နယူတန္ဟာ three law of motion ေရြ႕လ်ားျခင္းနိယာမသံုးမ်ိဳးကို ခ်ျပခဲ႔ပါတယ္ ။အဲဒီနိယာမေတြကို ရူပေဗဒ ရဲ့ အေျခခံ နိယာမေတြအျဖစ္လည္း လူသိမ်ားပါတယ္ ။
နိယာမ (၁)
အရာဝထၳဳေတြေပၚမွာ သက္ေရာက္တဲ႔အား (ေျမဆြဲအားနဲ႔ ပြတ္တိုက္အားမပါဝင္)မရွိဘူးဆိုရင္ အဲဒီအရာဝထၳဳေတြဟာ ပံုမွန္ အလ်င္(velocity) နဲ႔ပဲ ေရြ႕လ်ားေနမယ္ ။ (constant speed နဲ႔ သူ႔ရဲ့ဦးတည္ရာတိုင္းေရြ႕လ်ားေနတာျဖစ္နိုင္သလို ၊ ရပ္ေနတာ ၊ ထိုင္ေနတာမ်ိဳးလည္းျဖစ္နိုင္ပါတယ္)
ပထမ နိယာမရဲ့ ဥပမာေလးၾကည့္ၾကည့္ပါ ။ တကယ္လို႔သာ သက္ေရာက္တဲ႔အား မရွိခဲ႔ဘူးဆုိလွ်င္ ( f=0 ) အခ်ိန္ တိုင္းမွာေျပာင္းလဲမဲ႔ အလ်င္ (dv/dt) ကလည္း သုညပါပဲ တဲ႔ ။
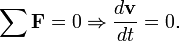
နိယာမ (၂)
အရာဝထၳဳတစ္ခုေပၚမွာသက္ေရာက္တဲ႔အား(f)ဟာ အဲဒီအရာဝထၳဳရဲ့ အေလးခ်ိန္ (m) ႏွင္႔ အရွိန္္(a) တို႔ေျမွာက္ျခင္းနဲ႔ ညီပါတယ္ ။
ဒုတိယနိယာမရဲ့သခ်ာၤဆိုင္ရာဥပမာေလး ၾကည့္ၾကည္ပါ ။
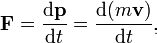
အရာဝထၳဳေပၚမွာသက္ေရာက္တဲ႔အားဟာ အဲဒီအရာဝထၳဳရဲ့ အခ်ိန္တိုင္းမွာေျပာင္းလဲသြားမဲ႔ linear momentum(p) နဲ႔ညီတယ္လို႔ ပထမေျပာပါတယ္ ။ အဲဒီ momentum ဟာ mass times velocity ဆိုတဲ႔ (mv) အခ်ိန္တိုင္းမွာျဖစ္ေပၚေျပာင္းလဲမဲ႔ အေလးခ်ိန္နဲ႔ အလ်င္ တ႔ိုႏွင္႔ ညီပါတယ္ ။
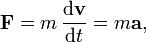
အလ်င္သာ အခ်ိန္တိုင္း အခ်ိန္တိုင္းမွာ ကိန္းရွင္အေနနဲ႔ ေျပာင္းသြားမယ္ အရာဝထၳဳရဲ့ အေလးခ်ိန္ (mass) ကေတာ႔ ဒီတိုင္းပါပဲ ။ ဒါေၾကာင္႔ f=m dv/dt လို႔ ေရးတာပါ ။ အခ်ိန္တိုင္း အခ်ိန္တိုင္း မွာ ေျပာင္းလဲမဲ႔ အလ်င္ဟာ အဲဒီအရာဝထၳဳရဲ့ အရွိန္ ပါပဲ ။ ဒါေၾကာင္႔ dv/dt = a ပါ ။ ေနာက္ဆံုးမွာေတာ႔ ဒုတိယ နိယာမ ေဖာ္ျမဴလာျဖစ္တဲ႔ f=ma ဆိုတာကို ရလာတာျဖစ္ပါတယ္ ။
နိယာမ (၃)
အရာဝထၳဳ ၂ ခုအခ်င္းခ်င္းတစ္ခုေပၚတစ္ခု သက္ေရာက္တဲ႔အားဟာ ပမဏတူညီၿပီးေတာ႔ ဦးတည္ရာ မတူဘူး ။
ၿဂိဳလ္ေတြရဲ့ ေရြလ်ားမွဳကို ရွင္းျပနိုင္ဖို႔အတြက္ေတာ႔ နယူတန္ဟာ သူ႔ရဲ့ အေျခခံ နိယာမ ၃ ခုကႏွင္႔ ေျမဆြဲအားနိယာမ ကို ေပါင္းစပ္အသံုးျပဳခဲ႔ပါတယ္ ။
ေျမဆြဲအားနိယာမ
အရာဝထၳဳ ႏွစ္ခု ၾကားမွာရွိတဲ႔ ေျမဆြဲအားဟာ အဲဒီအရာဝထၳဳ ႏွစ္ခုရဲ့ အေလးခ်ိန္ေတြ ေျမွာက္ျခင္းနဲ႔ တိုက္ရိုက္အခ်ိဳးက်ၿပီးေတာ႔ ၊ အရာဝထၳဳႏွစ္ခုၾကားမွာရွိတဲ႔ အကြာေဝး ၂ ဆ နဲ႔ ေျပာင္းျပန္အခ်ိဳးက်တယ္။
နယူတန္ရဲ့ နိယာမ ေတြဟာ က ကပ္ပလာ နိယာမေတြထက္ ပိုမိုရုိးရွင္းၿပီးနားလည္ရလြယ္ကူေစပါတယ္ ။ ဒါေပမဲ႔လည္း အဲဒီ နိယာမေတြဟာ ကပ္ပလာရဲ့ ေတြးေခၚမွဳ ရလဒ္ ေတြလို႔လည္းဆိုနိုင္ပါတယ္ ။
နယူတန္ရဲ့ စၾကာဝဠာသေဘာဟာ တခါတေလမွာ ခ်ိန္သီးနာရီေတြရဲ့ အလုပ္လုပ္ပံုကဲသုိ႔ေဖာ္ျပၿပီးေတာ႔ ဘာခ်ိန္မွာဘာျဖစ္မယ္ ၊ ဘာေတြျဖစ္လိမ္႔မယ္ဆိုတာ ႀကိဳတင္ေဟာကိန္းထုတ္နိုင္တယ္လို႔ဆိုပါတယ္ ။ ကၽြန္ေတာ္တို႔ ဟာ ဘိလိယက္ေဘာလံုးေလးေတြ အခ်င္းခ်င္းထိတိုက္ၿပီး ဘယ္ေနရာကုိေရြ႕မယ္ဆိုတာ ႀကိဳတင္မွန္းဆနိဳင္သလုိပါပဲ ။ ေယဘုယ်အားျဖင္႔ေတာ႔ ကၽြန္ေတာ္တို႔ဟာ ဟန္ပန္ ၊ သ႑န္ေတြ တူညီမွုကိုၾကည့္ၿပီးခန္႔ မွန္းနုိင္ၾကတာပါ ။ ၿဂိဳလ္ေတြဟာလည္း ဘိလိယက္ေဘာေတြလို ပံု သ႑န္ေတြ ႏွင္႔ ေရြ႕လ်ားမွုေတြ တူညီေနပါတယ္ ။
ရုတ္တရက္ဆိုသလိုပဲ အာကာသ မွာရွိေနတဲ႔ ရွဳပ္ေထြးလွတဲ႔ ေရြ႕လ်ားမွုေတြကေန သခ်ာၤနည္းစနစ္ေတြရဲ့ ရိုးရွင္းတဲ႔ ဆင္႔ကဲေျပာင္းလဲမွဳေတြအျဖစ္ျပသနိုင္ခဲ႔ပါတယ္ ။ ဒါဟာလူသားေတြရဲ့ နားလည္နိုင္မွဳ ကို ပိုမို ယံုၾကည္ေစခဲ႔တာပါပဲ ။ ကမၻာရဲ့ ပတ္ပတ္လည္ကို ထိန္းခ်ဳပ္နိုင္ဖို႔ စြမ္းရည္ေတြလည္းရရွိေစခဲ႔တယ္ ။ ကပ္ပလာနဲ႔ နယူတန္ တို႔ရဲ့ ေတြ႔ ရွိမွုဟာ နကၡတ္ ေဗဒ တစ္ခုတည္းတင္ေျပာင္းလဲေစခဲ႔တာမဟုတ္ပဲ ၊ စၾကၤဝဠာနဲ႔ပက္သက္ၿပီး လူေတြရဲ့ ယူဆခ်က္အျမင္ေတြကိုပါေျပာင္းလဲေစခဲ႔တယ္ ။
နယူတန္ရဲ့ ေလ႔လာေတြ႔ရွိခ်က္ဟာ ႀကီးက်ယ္ခမ္းနားေပမဲ႔လည္း ၿပီးျပည့္စံုသြားတာေတာ႔မဟုတ္ပါဘူး။ နယူတန္ရဲ့ နိယာမ ဟာ ေျမဆြဲအား အေၾကာင္းကို ျပည့္စံုေအာင္ရွင္းမျပနိုင္ခဲ႔ပါဘူး ။ နယူတန္ဟာ ေျမဆြဲအားရဲ့ ပမာဏ ဘယ္ေလာက္ရွိသလဲဆိုတာ သခ်ာၤ နည္းအရာ တိတိ က်က် ျဖစ္ေအာင္ ကိုတြက္ထုတ္ျပခဲ႔ပါတယ္ ။ ဒါေပမဲ႔ ကမၻာေျမဆြဲအားဘာေၾကာင္႔ျဖစ္ေစ သလဲ ဆိုတာကိုေတာ႔ သူရွင္းမျပနိုင္ခဲ႔ပါဘူး ။ ကမၻာေျမရဲ့ဆြဲအားဟာဘယ္လိုမ်ိဳးပါလဲ ၿဂိဳလ္တစ္ခုနဲ႔တစ္ခုၾကားမွာ ႀကိဳလိုမ်ိဳးတြယ္ဆက္ၿပီး တစ္ခုႏွင္႔တစ္ခု ဆြဲေနၾကတာမ်ိဳးလား ။ သံုးသပ္ၾကည့္ရတာကေတာ႔ အဲလိုမျဖစ္နိုင္ပါဘူး ။ ေျမဆြဲအားဘယ္လို အလုပ္လုပ္လဲဆိုတာ ယခုေခတ္အခ်ိန္ခါမွာေတာ႔ ပိုသိလာၾကပါၿပီ ။ ဒါေပမဲ႔ နယူတန္ ေခတ္တုန္းကေတာ႔ ဒါကိုမသိခဲ႔ၾကေသးပါဘူး။ဒါေၾကာင္႔လည္းနယူတန္ ေျမဆြဲအားနိယာမကို ေဖာ္ထုတ္တဲ႔အခါမွာသြယ္ဝိုက္ၿပီးထုတ္ခဲ႔တာပဲျဖစ္ပါတယ္ ။ ကၽြန္ေတာ္တို႔ အသံုးျပဳ နိုင္ဖို႔ အတြက္ဆိုရင္ေတာ႔ အရာရာ တိုင္းကို ၿပီးျပည့္စံုေအာင္ ရွင္းလင္းဖို႔မလိုအပ္လွပါဘူး။ ဒါဟာ နည္းပညာ (technology) ႏွင္႔ သိပၸံပညာ (Science) ေတြအတြက္ ဆင္႔ကဲ ေျပာင္းလဲျခင္းေတြျဖစ္ေပၚေစတဲ႔ အခ်က္ေတြပါပဲ ။
ကဲ႔ကုလပ္စ္ဆိုတာလည္း အဲဒီအတိုင္းပါပဲ ။ နယူတန္နဲ႔ လစ္ဘနစ္စ္ တို႔ဟာ ေယဘုယ်ဖန္ရွင္ေတြကိုဘယ္လို derivates လုပ္ရမယ္ဆိုတာကို ေကာင္းေကာင္းသိခဲ႔ၾကပါတယ္။ ဒါေပမဲ႔ derivative ရဲ အဓိပၸါယ္ဖြင္႔ဆိုခ်က္ကိုေတာ႔ တိတိ က်က် မေျပာျပခဲ႔ၾကဘူး ။ သူတို႔ဟာသူတို႔အသံုးျပဳ ခဲ႔တဲ႔ သီအိုရမ္ေတြကို တကယ္မေျဖရွင္းနိုင္ခဲ႔ၾကဘူး ။ သူတို႔ရဲ့ေဖာ္ျပခ်က္ေတြဟာရွင္းျပခ်က္ေတြမဟုတ္ဘူး ။ သူတို႔ဟာ derivative ကို အလြန္အလြန္ေသးငယ္တဲ႔ ဂဏန္း၂ ခုရဲ့ စားလဒ္ အျဖစ္ပဲ ရွင္းျပခဲ႔ၾကတယ္ ။ (ဥပမာ ..အဲဒီဂဏန္းေတြဟာ အဆံုးဆမရွိ ေသးငယ္တယ္ ၊ ဒါေပမဲ႔ သုညလည္းမဟုတ္ျပန္ဘူး)အဲဒီရွင္းလင္းေဖာ္ျပခ်က္ဟာအဲဒီအခ်ိန္ကသခ်ာၤပညာရွင္ေတြကိုသိပ္ၿပီးသေဘာမေတြ႔ေစခဲ႔ပါဘူး ။ ဒါေပမဲ႔လည္း နယူတန္ နဲ႔ လစ္ဘနစ္စ္ တို႔ရဲ့ တြက္ခ်က္မွဳ နည္းလမ္းဟာ အေျဖ မွန္ ထြက္ဖို႔ အတြက္ေတာ႔ အမွားေထာက္ျပစရာမရွိေလာက္ရွင္းလင္းနိုင္ခဲ႔ပါတယ္ ။
ေနာင္ ႏွစ္ေပါင္း ၂၀၀ ေလာက္ၾကာၿပီးတဲ႔ေနာက္မွာေတာ႔ ဂ်ာမန္ သခ်ာၤပညာရွင္ ဝဲရာစထရက္စ္ (Weierstrass- 1815 –1897) ႏွင္႔ ျပင္သစ္သခ်ာၤပညာရွင္ ေကာ႔ေခ် (Cauchy-၁၇၈၉-၁၈၅၇) တို႔ ကေတာ႔ ကဲကုလပ္စ္ရဲ့ နည္းစနစ္တစ္မ်ိဳးျဖစ္တဲ႔ (epsilons and deltas) ဆိုတဲ႔ ပိုေကာင္းတဲ႔ စနစ္ ကို ထုတ္ေဖာ္နိုင္ခဲ႔ပါတယ္ ။ ဒယ္လ္တာနဲ႔ အပ္စလြန္ နည္းကေတာ႔ ေသးငယ္တဲ႔ ဂဏန္းပမာဏကို လက္ေတြျပသနိုင္ဖို႔ နည္းစနစ္ပါ ။
၁၉၆၀ ခုႏွစ္မွာေတာ႔ ယုတၱိေဗဒ ပညာရွင္ ေအဗရာဟမ္ ရိုဘင္ဆမ္ ဟာ အလြန္တိုေတာင္းတဲ႔အခ်ိန္ပမာဏေလး(infinitesimals)အာရံုခံေဖာ္ျပနိုင္မဲ႔နည္းလမ္းကိုေတြ႔ရွိခဲ႔ပါတယ္ ။ ဒါသာသခ်ာၤဘာသာရပ္ရဲ့ အစိတ္အပိုင္းအသစ္ျဖစ္တဲ႔ nonstandard analysis ပါပဲ ။ nonstandard analysis ဟာ calculus ေတြ ၊ differential equation ေတြ ႏွင္႔ ၄င္းတို႔နဲ႔ဆက္ႏႊယ္ေနတဲ႔ အေၾကာင္းအရာေတြကို နားလည္နိုင္ဖို႔ ပိုေကာင္းတဲ႔နည္းလမ္းတစ္ခုပါပဲ။ ဒီနည္းလမ္းဟာ ဘယ္လိုပံုစံလဲဆိုေတာ႔ အေၾကာင္းရာတစ္ခုကို အေျခေန ၊ ရွင္းျပခ်က္ေတြ နဲ႔ သိတာထက္ မသိစိတ္ကေန အလိုလိုသိတဲ႔ ၊ ဝမ္းတြင္းသိ အေနနဲ႔လက္ခံလိုက္တာမ်ိဳးပါ ။ နယူတန္နဲ႔ လစ္ဘနစ္ဇ္ တို႔ဟာ ကဲကုစ္လဗ္ စ္ ကို စိတ္ထဲကအေနအလိုလိုသိေနၾကတယ္လို႔ယူဆလိုက္တာမိ်ဳးပါ။အေျခခံအားျဖင္႔ ေတာ႔ ဒါဟာ infinitesimal approach ႏွင္႔ epsilon-delta approach တို႔ရဲ့ အႀကီးမားဆံုးကြားျခားခ်က္ပါပဲ ။
Delta-epsilon နည္းလမ္းမွာဆိုရင္ ဂဏန္းေတြဟာ သတ္မွတ္တဲ႔ အရြယ္အစားတစ္ခုရွိၾကတယ္။ ေတြးၾကည့္မယ္ဆိုရင္ပမာဏတစ္ခုရွိတဲ႔ဂဏန္းဟာလံုးဝအေသးငယ္ဆံုးေတာ႔မဟုတ္ေသးဘူး။ထပ္ၿပီးေျပာင္းလဲနိုင္ေသးတဲ႔ေသးငယ္မွဳမ်ိဳးပဲ ။ ဥပမာတစ္ခုေပါ႔ တစ္ရဲ့ တစ္သန္းပံုပံု တစ္ပံု ရွိတဲ႔ ပမာဏေလးဆိုပါေတာ႔ ။ အဲဒီဂဏန္းေလးကို အေသးဆံုး ျဖစ္ေအာင္ဆက္လုပ္မယ္ဆိုရင္ ဘာေတြျဖစ္လာမလဲ ။ ဒီဂဏန္းဟာ ေျပာင္းလဲသြားမယ္ ။ အဲလိုေျပာင္း လဲေနတာဟာ montion တစ္ခု action တစ္ခု လို႔ဆိုနိုင္မလား ။ ကကုလဗ္စ္ရဲ့ သေဘာတရားက အခ်ိန္တိုင္းအခ်ိန္တိုင္း ၊ အေရြးတိုင္းအေရြ ႔တိုင္းမွာ ေျပာင္းလဲ မွဳကိုသိနိုင္ဖို႔အတြက္ အေသးငယ္ဆံုး ခ်ံဳ႕ၿပီး တြက္ခ်က္တာ ပါ ။ အေသးငယ္ဆံုးျဖစ္ေအာင္ခ်ံဳ႕တဲ႔ေနရာမွာလဲ ေျပာင္းလဲသြားနိုင္တယ္ ။
ဒါေၾကာင္႔ နယူတန္ ၊ လစ္ဗနစ္ နဲ႔ ရိုဘင္ဆမ္ တို႔ဟာ လံုးဝ ထပ္ေသးစရာမလိုေတာ႔တဲ႔ အေသးဆံုး ဂဏန္း infinitesimals အျဖစ္ စိတ္ထဲမွာသတ္မွတ္လိုက္တာပါ ။ ဒါဆိုရင္ အဲဒီဂဏန္းဟာ ထပ္ၿပီး ေသးေအာင္ေျပာင္းလဲဖို႔မလိုေတာ႔ပါဘူး ။ ဘယ္လိုလဲဆိုေတာ႔ အေသးငယ္ဆံုးေသာဏဂန္း ဒါေပမဲ႔ ပမာဏေတာ႔ေဖာ္ျပလို႔ မရဘူးဆိုတဲ႔ပံုစံေပါ႔ ။ ဒါဟာ သခ်ာၤရဲ့ ႀကီးမားတဲ႔ အစိတ္ပိုင္းသစ္ပါပဲ ။
၁၉ ရာစုေႏွာင္းပိုင္းမွာေတာ႔ ေဂ်ာ႔ခန္တား(Georg Cantor) ဟာ infinity ဆိုတဲ႔ ေဝါဟာရတစ္ခု ႏွင္႔ သူ႔ရဲ့ အယူအဆေတြ ကို ထုတ္ေဖာ္ခဲ႔ပါတယ္ ။ ခန္းတား ဟာ convergence of Fourier series ကိုေလ႔လာခဲ႔တယ္ ။ အေစာပိုင္းသခ်ာၤပညာရွင္ေတြဟာ တူညီတဲ႔ အစုေတြ ျပဳၿပီးေတာ႔ ပဲ မေရမတြက္နိုင္တဲ႔ ဂဏန္း ေတြကိေဖာ္ျပၾကတယ္ ။ ဒါေပမဲ႔ ခန္းတား ကေတာ႔ အဲေလာက္နဲ႔ရပ္မထားပါဘူး ။ တကယ္လို႔ sets ေတြမွာ ပါဝင္တဲ႔ elements အေရအတြက္ (cardinality) သာတူညီခဲ႔မယ္ဆိုရင္ အဲဒီ set ေတြကို အခ်ိဳးခ်ၿပိးေတာ႔လည္းေရးနိုင္ပါေသးတယ္ ။အဲဒီလိုေဂ်ာ႔ခန္းတား ဟာ infinity set ႏွစ္ခုကို အခ်ိဳးခ်လိုက္တဲ႔ ေနာက္ပိုင္းမွာ ေတာ႔ ကၽြန္ေတာ္တို႔ မ်က္ျမင္ နဲ႔ ေရတြက္နိုင္မဲ႔ countable numbers ႏွင္႔ အတူ မ်က္ျမင္နဲ႔ ေဖာ္ျပလို႔ မရတဲ႔ uncountable numbers ေတြပါရွိေသးတယ္ဆိုတာကိုလူေတြ လက္ခံလာၾကပါတယ္။
သက္ေသျပနိုင္တဲ႔ နည္းစနစ္ေတြ တိုးတက္လာတာနဲ႔ အမွ် သခ်ာၤရဲ့ အခန္းက႑ဟာလည္းပိုၿပီးအေရးပါလာခဲ႔တယ္ ။ ပိုၿပီးေတာ႔ လက္ေတြ႔နယ္ပယ္နဲ႔ ဆက္စပ္လာနိုင္တယ္ ၊ ပိုၿပီးေတာ႔လည္းတိက်လာၾကတယ္ ။ ဒီကေန႔ ကၽြန္ေတာ္တို႔ ရဲ့ သခ်ာၤအဆင္႔အတန္းဟာေတာ႔ အလြန္ကိုျမင္႔မားေနပါၿပီ ။ ဒါဟာ ဘယ္ကေနျဖစ္ေပၚလာရသလဲဆိုရင္ “ အေၾကာင္းျပခ်က္ ရွာေဖြျခင္းအတက္ပညာကေနရရွိလာတာပါ ” ။ ရုပ္ပုိင္းဆိုင္ရာ ေလ႔လာမွဳကေနေတြ႔ရွိခဲ႔တာမဟုတ္ပါဘူး ။ ကၽြန္ေတာ္တို႔ ဟာ သခ်ာၤကို အဆင္႔တစ္ဆင္႔ခ်င္းဆီမွာ တိက်တဲ႔ အေၾကာင္းျပခ်က္ေတြရွာေဖြၿပီး ေဖာ္ျမဴလာေတြထုတ္ခဲ႔ၾကတယ္ ။ အဲ ဒီထုတ္ခဲ႔တဲ႔ ေဖာ္ျမဴလာေတြအတိုင္း လက္ေတြ႔နယ္ပယ္မွာ အသံုးခ်ခဲ႔ၾကတယ္ ။
ဥပမာ အေနနဲ႔ ခဲတံတစ္ခုနဲ႔ စာရြက္ပိုင္းတစ္ခုေပၚမွာ မ်ဥ္းတစ္ေၾကာင္းဆြဲလိုက္ပါ ။ အဲဒီစာရြက္ဟာ တစ္လက္မေလာက္ပဲရွည္ခ်င္ရွည္ပါလိမ္႔မယ္ ။ ၿပီးေတာ႔ မ်ဥ္ရဲ့ အစြန္းတစ္ဖက္ကို 0 လု႔ိ မွတ္ၿပီး ၊ ေနာင္စြန္းတစ္ဖက္ကို 1 လု႔ိ မွတ္လိုက္ပါ ။ အဲဒီမ်ဥ္းေၾကာင္းေလးရဲ့ အပိုင္းေလး ဟာ [0,1] ပါ။ ဒါေပမဲ႔ ေနာက္ ထပ္ မ်ဥး္ကိုအဆံုးဆမရွိ ဆက္ဆြဲနိုင္ပါေသးတယ္ ။အဆံုးအဆမရွိတဲ႔ အမွတ္ေတြလည္းရွိေနပါေသးတယ္ ။ ဒါေပမဲ႔ စာရြက္ဟာ ကန္႔သတ္ခ်က္ျဖစ္ေနပါတယ္ ။ မ်က္ျမင္ကမၻာ ဟာလည္း စာရြက္အပိုင္းလိုပါပဲ ။ ကၽြန္ေတာ္တို႔ အျမင္ေတြကန္႔သတ္မွဳေတြ ရွိေနေပမဲ႔ အေတြးအေခၚမ်ဥ္းေတြေတာ႔ ဆက္ဆြဲ လို႔ရေနပါေသးတယ္ ။ ဒါေပ မဲ႔ အဲဒီအေတြးအေခၚမ်ဥ္းေတြကို လက္ေတြ႔ (ျမက္ျမင္ကိုယ္ေတြ႔) ကမၻာမွာ ခ်ျပလို႔ရနိုင္ေအာင္ ၊ ရွင္းျပလို႔ရနိုင္ေအာင္ ေပါင္းကူးေပးမဲ႔အရာ တစ္ခု ရွိေနပါတယ္ ။ အဲဒါကေတာ႔ ကၽြန္ေတာ္တို႔ သင္ၾကားခဲ႔ရတဲ႔ ကာကုလပ္စ္ ဆိုတဲ႔ အရာႀကီးပါပဲ ။
ကနဦးအစ ကကၽြန္ေတာ္ေျပာခဲ႔သလိုပါပဲ ။ ကဲကုလပ္စ္ ဟာ ဒါႀကီးပါလို႔ လက္ဆုပ္လက္ကိုင္ ျပလို႔ရတဲ႔အရာ မဟုတ္ပါဘူး ။ tutorial ေတြ ၊ training course ေတြလို ဒါ ၿပီးရင္ဒါလုပ္ဆိုတဲ႔ ပညာရပ္မ်ိဳးလည္းမဟုတ္ပါဘူး ။ဆက္စပ္ ျဖစ္ေပၚလာတဲ႔ ေတြးေခၚမွဳမ်ိဳးပါ ။ ဒါေၾကာင္႔ ကဲကုလပ္စ္ မေပၚခင္ ကစလို႔ သခ်ာၤသမိုင္းအနည္းအက်ဥ္းကို အရွည္ႀကီးေျပာျပခဲ႔တာပါ ။ အေပၚကစာေတြ ဖတ္ၿပီးတဲ႔ခါ ကဲကုလပ္စ္ဟာ ဘယ္လိုအရာလည္းအနည္းငယ္သေဘာေပါက္မယ္ထင္ပါတယ္ ။ (ကၽြန္ေတာ္႔စာအေရးသားကိုကၽြန္ေတာ္သိလု႔ိ နည္းနည္းနားလည္လိမ္႔မယ္ထင္တယ္လို႔ေျပာတာေနာ္ … စာဖတ္သူကိုအထင္ေသးလို႔မဟုတ္ပါ … း) …. )
ကဲကုလပ္စ္ ရဲ့ လက္တင္ဘာသာ အဓိပၸါယ္ကေတာ႔ ေရတြက္ရမွာသံုးတဲ႔ ေက်ာက္တံုးအေသးစားေလးလို႔ အဓိပၸါယ္ရပါတယ္ ။ ကဲကုလပ္စ္မွာ Limit , differentiate,integral,infinite စတဲ႔အပိုင္းေတြ ပါဝင္ပါတယ္ ။ သိုေပမဲ႔ အဓိက သေဘာတရားကေတာ႔ differential , integral တို႔ပါပဲ ။ differential ရဲ့ သေဘာကေတာ႔ ကၽြန္ေတာ္တို႔ အေတြးအေခၚေတြ ကို တကယ္႔ လက္ေတြ႔နယ္ပယ္နဲ႔ ဆက္စပ္နိုင္ဖို႔ ခ်ံဳ႕ ယူလိုက္တာပါ ။ ၿပီးတဲ႔ အခါမွာ ကၽြန္ေတာ္တုိ႔ အငယ္ဆံုးတန္ဖိုးေတြရလာမယ္ ။ ေဖာ္ျမဴလာေတြ ၊ အီေကြးရွင္းေတြ အျဖစ္ထုတ္ၾကမယ္ ။ အဲဒီရလာတဲ႔ေဖာ္ျမဴလာေတြ အီေကြးရွင္းေတြ ကို တခါ ျပန္ၿပီးေျပာင္းျပန္ေပါ႔ ျပန္ခ်ဲ႕ ၾကည့္ဖို႔ က်ေတာ႔ အင္တီဂရိတ္ကိုသံုးပါတယ္ ။ ဒါေၾကာင္႔ ကၽြန္ေတာ္ လိုလူၿပိန္း အေနနဲ႔ မွတ္သားမယ္ဆိုရင္ေတာ႔ differentiate ဆိုတာခ်ံဳ႔ၾကည့္တာ ၊ integrate ဆိုတာျပန္ခ်ဲ႔ ၾကည့္တာ ပါပဲ (တကယ္ တိတိက်က် ေလ႔လာမယ္ဆိုရင္ေတာ႔ ဒီထက္ပိုနိုင္ပါတယ္ ၊ ကၽြန္ေတာ္ ကသေဘာတရားကိုပဲ ဆိုလိုတာပါ ) ။
ကဲကုလပ္စ္ ကိုဘယ္ေနရာေတြမွာ သံုးလဲ ။ သေဘာတရား ကေတာ႔ သိပၸံ ပညာ ရဲ့ နယ္ပယ္စံုမွာ သံုးတယ္လို႔ ဆိုရပါ႔မယ္ ။ ဘာရည္ရြယ္ခ်က္နဲ႔ သံုးလဲဆိုေတာ႔ အေပၚမွာ ေျပာခဲ႔သလိုပါပဲ ကၽြန္ေတာ္တို႔ မ်က္ျမင္ မေတြ႔ နိုင္တဲ႔ အရာေတြကို လက္ေတြ ျပသဖို႔ နဲ႔ ကၽြန္ေတာ္တို႔ လက္ေတြ႔ မႀကံဳရေသးတဲ႔ အေျခေနေတြကို တိက်မွန္ကန္တဲ႔ နည္းလမ္းေတြ နဲ႔ ႀကိဳတင္ခန္႔မွန္းနိုင္ဖို႔ပါပဲ ။ ဥပမာ ေပါ႔ ကားတစ္စီးက တစ္မိနစ္ကို ၁၀ မိုင္ ခရီးေရာက္တယ္လို႔ ဆိုပါေတာ႔၊ မိုင္ ၁၀၀ ဆို အခ်ိန္ဘယ္ေလာက္နဲ႔ ေမာင္းနိုင္မလဲ ကၽြန္ေတာ္တို႔ ႀကိဳတင္ခန္႔မွန္းလို႔ရပါၿပီ ။ အလားတူ ကဲကုလပ္စ္ သေဘာတရား ေတြ နဲ႔ ပဲ ကမၻာႀကီးဟာ speed ဘယ္ေလာက္နဲ႔ ေနကိုလွည့္ပတ္ေနသလဲ ၊ ကမၻာ ရဲ့ ေနကိုပတ္တဲ႔ ပတ္လမ္းဟာ ဘယ္ေလာက္ အတိုင္းတာရွိသလဲဆိုတာကို ကၽြန္ေတာ္တို႔လူေတြသိနိုင္ခဲ႔တာပါ ။ ကမၻာ ႀကီးအျပင္ဘက္ကို လူေတြ ထြက္ၿပီး ၊ ကမၻာႀကီး ပတ္တဲ႔လမ္းအတိုင္ း ေနကို ပတ္ခ်ာလွည့္တိုင္းလို႔ သိခဲ႔ၾကတာမဟုတ္ဘူး ။ ေနာက္ Control systems ေတြ တည္ေဆာက္ရာ ၊ အာကာသယာဥ္ေတြ ၊ ေလယာဥ္ေတြ တည္ေဆာက္ရာ မွာ လူကိုယ္တိုင္လိုက္ပါ စမ္းသပ္မယ္ဆုိရင္ မလိုအပ္ပဲ လူေတြ အသက္ေတြဆံုးရွံုးမယ္ ၊ အရင္းႏွီး မ်ားႀကီးေပးဆပ္ရနိုင္တယ္ ။ အဲဒီ အခ်ိန္ေတြမွာ ဘာလုပ္လဲ ကဲကုလပ္ ကိုသံုးၿပီး mathematical model ေတြ တည္ေဆာက္တယ္ ၊ ကြန္ျပဴတာနဲ႔ visualized လုပ္ၿပီးေတာ႔ simulation ေတြ လုပ္ၾကည့္မယ္ ။ တိက် ၊ မွန္ကန္တဲ႔ရလဒ္ေတြထြက္လာတဲ႔အခါမွ လက္ေတြ႔မွာတည္ေဆာက္တယ္ ။ ဒါဆိုရင္ ဆံုးရွံဳးမွုလည္းနည္းမယ္ ၊ ျမန္လည္းျမန္ဆန္မယ္ ။ ဒါေတြ ဟာ ကဲကုလပ္စ္ ကေနရလာတဲ႔ အက်ိဳးေက်းဇူးေတြပဲျဖစ္ပါတယ္ ။
ကဲဗ်ာ ဒီေလာက္ဆိုရင္ေတာ႔ ကၽြန္ေတာ္တို႔ေက်ာင္းသားေတြ ၊ ဗဟုသုတရွာေဖြသူေတြအေနနဲ႔ ကဲကုလပ္စ္ကို ဘာေၾကာင္႔ သင္ေနၾကရလဲ ၊ ေလ႔လာေနၾကရလဲ ၊ ကဲကုလပ္စ္ ဆိုတာဘာလဲ ၊ ကဲကုလပ္စ္ရဲ့ သေဘာသဘာဝကေရာဘာလဲ ၊ ကဲကုလပ္စ္ကို ဘယ္ေနရာေတြမွာအသံုးခ်လဲ ဆိုတာ ဗဟုသုတရၾကလိမ္႔မယ္လို႔ထင္ပါတယ္ ။ ကၽြန္ေတာ္ဟာ သခ်ာၤပညာရွင္မဟုတ္တဲ႔အတြက္ ကၽြန္ေတာ႔ေရးသားမွဳမွာ အမွားေတြပါေကာင္းပါနိုင္ပါတယ္ ။ ဒါေပမဲ႔ ပညာရပ္တစ္ခုအတြက္ ဗဟုသုတေလး ရသြားတယ္ဆိုရင္ ကၽြန္ေတာ္ေရးသားရက်ိဳးနပ္တယ္လို႔ခံယူပါတယ္ ။ ကဲကုလပ္ကိုလက္ေတြ႔ အသံုးခ်မွု နဲ႔ ဆက္စပ္တာေလးေတြေတာ႔ အခ်ိန္ရရင္ ထပ္ေရးသားပါဦးမယ္ ။
by ၇ုပ္ဆိုး
ကိုးကား
http://wikimyanmar.co.cc/wiki/index....80%95%E1%80%B9
http://www.math.vanderbilt.edu/~sche.../whystudy.html
http://en.wikipedia.org/wiki/Calculus
http://www.calculus.org/
No comments:
Post a Comment